Question

17．已知定义在R上的函数f（x）满足①图象关于（1，0）点对称；②f（-1+x）=f（-1-x）；③x∈[-1，1]时，f（x）=$\left\{\begin{array}{l}{1{-x}^{2}，x∈[-1，0]}\\{cos\frac{π}{2}x，x∈（0，1]}\end{array}\right.$，则函数y=f（x）-（$\frac{1}{2}$）^|x|在区间[-3，3]上的零点个数为5．

Answer 1

分析 由①可得f（x）+f（2-x）=0，求得x在[1，3]上的f（x）的解析式；再由②求得x在[-3，-1]上的解析式，画出f（x）和y═（$\frac{1}{2}$）^|x|在[-3，3]的图象，通过图象观察，可得它们有5个交点，即可得到零点的个数．

解答 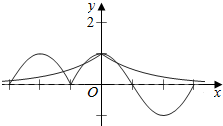解：由题意可得f（x）+f（2-x）=0，
当1≤x≤2时，0≤2-x≤1，f（2-x）=cos$\frac{π}{2}$（2-x）=-cos$\frac{π}{2}$x，
则f（x）=-f（2-x）=cos$\frac{π}{2}$x；
当2＜x≤3时，-1≤x＜0，f（2-x）=1-（2-x）²，
则f（x）=-f（2-x）=（2-x）²-1．
由②f（-1+x）=f（-1-x），即为f（x）=f（-x-2），
当-3≤x≤-2时，0≤-2-x≤1，f（-2-x）=cos$\frac{π}{2}$（-2-x）=-cos$\frac{π}{2}$x，
则f（x）=-f（-2-x）=-cos$\frac{π}{2}$x；
当-2＜x≤-1时，-1≤-2-x＜0，f（-2-x）=1-（-2-x）²，
则f（x）=f（-2-x）=1-（-2-x）²．
y=f（x）-（$\frac{1}{2}$）^|x|在区间[-3，3]上的零点
即为y=f（x）和y=（$\frac{1}{2}$）^|x|在[-3，3]的交点个数．
作出y=f（x）和y═（$\frac{1}{2}$）^|x|在[-3，3]的图象，
通过图象观察，可得它们有5个交点，
即有5个零点．
故答案为：5．

点评 本题考查函数的性质和运用，考查函数方程的转化思想，注意运用数形结合的思想方法，属于中档题．