题目内容
2．已知数列{an}中，a1=1，an+1=$\frac{2{a}_{n}}{2+{a}_{n}}$（n∈N*），则可归纳猜想{an}的通项公式为（ ）| A． | an=$\frac{2}{n}$ | B． | an=$\frac{2}{n+1}$ | C． | an=$\frac{1}{n}$ | D． | an=$\frac{1}{n+1}$ |
分析 写出前几项，即可归纳猜想{an}的通项公式．
解答 解：∵a1=1，an+1=$\frac{2{a}_{n}}{2+{a}_{n}}$，
∴a2=$\frac{2}{3}$，a3=$\frac{\frac{4}{3}}{2+\frac{2}{3}}$=$\frac{2}{4}$，
归纳猜想{an}的通项公式为an=$\frac{2}{n+1}$，
故选B．
点评 本题考查归纳猜想{an}的通项公式，考查学生的计算能力，正确计算是关键．
练习册系列答案
相关题目
13．
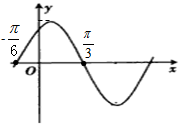函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象向左平移$\frac{π}{12}$单位得到的部分图象如图，则φ=（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象向左平移$\frac{π}{12}$单位得到的部分图象如图，则φ=（ ）| A． | $\frac{π}{6}$ | B． | -$\frac{π}{6}$ | C． | $\frac{2π}{3}$ | D． | $\frac{π}{2}$ |
10．若θ是直线l的倾斜角，且sinθ+cosθ=$\frac{{\sqrt{5}}}{5}$，则l的斜率为（ ）
| A． | -$\frac{1}{2}$ | B． | -$\frac{1}{2}$或-2 | C． | $\frac{1}{2}$或2 | D． | -2 |
17．直线y=a与y=2x-3及曲线y=x+ex分别交于A、B两点，则|AB|的最小值为（ ）
| A． | $\frac{3}{2}$ | B． | e | C． | 3 | D． | 2 |
7．按程序框图（如图）执行，输出的第4个数是（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |