题目内容
(本小题满分12分)
如图,已知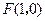 ,直线
,直线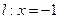 ,
,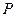 为平面上的动点,过点
为平面上的动点,过点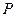 作
作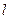 的垂线,垂足为点
的垂线,垂足为点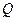 ,且
,且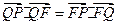 .
.
(Ⅰ)求动点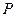 的轨迹
的轨迹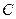 的方程;
的方程;
(Ⅱ)过点 的直线交轨迹
的直线交轨迹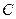 于
于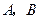 两
两 点,交直线
点,交直线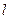 于点
于点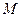 .
.
(1)已知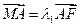 ,
,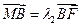 ,求
,求 的值;
的值;
(2)求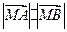 的最小值.
的最小值.
如图,已知
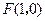 ,直线
,直线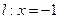 ,
,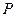 为平面上的动点,过点
为平面上的动点,过点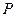 作
作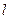 的垂线,垂足为点
的垂线,垂足为点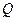 ,且
,且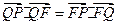 .
.(Ⅰ)求动点
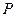 的轨迹
的轨迹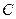 的方程;
的方程;(Ⅱ)过点
 的直线交轨迹
的直线交轨迹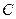 于
于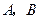 两
两 点,交直线
点,交直线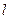 于点
于点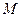 .
.(1)已知
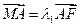 ,
,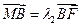 ,求
,求 的值;
的值;(2)求
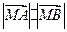 的最小值.
的最小值.(1)0
(2)16
解法一:(Ⅰ)设点 ,则
,则 ,由
,由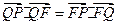 得:
得:

 ,化简得
,化简得 .
.
(Ⅱ)(1)设直线 的方程为:
的方程为:
 .
.
设 ,
, ,又
,又 ,
,
联立方程组 ,消去
,消去 得:
得: ,
, ,
,
 由
由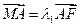 ,
,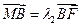 得:
得:

 ,
, ,整理得:
,整理得:
 ,
, ,
,



 .
.
解法二:(Ⅰ)由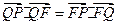 得:
得: ,
,
 ,
,  ,
,  .
.
所以点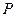 的轨迹
的轨迹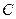 是抛物线,由题意,轨迹
是抛物线,由题意,轨迹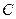 的方程为:
的方程为: .
.
(Ⅱ)(1)由已知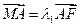 ,
,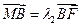 ,得
,得 .
.
则 :
: .…………①
.…………①
过点 分别作准线
分别作准线 的垂线,垂足分别为
的垂线,垂足分别为 ,
, ,
,
则有: .…………②
.…………②
由①②得: ,即
,即 .
.
(Ⅱ)(2)解:由解法一,



 .
.
当且仅当 ,即
,即 时等号成立,所以
时等号成立,所以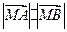 最小值为16.
最小值为16.
 ,则
,则 ,由
,由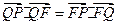 得:
得:
 ,化简得
,化简得 .
.(Ⅱ)(1)设直线
 的方程为:
的方程为: .
.设
 ,
, ,又
,又 ,
,联立方程组
 ,消去
,消去 得:
得: ,
, ,
, 由
由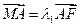 ,
,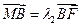 得:
得:
 ,
, ,整理得:
,整理得: ,
, ,
,


 .
.解法二:(Ⅰ)由
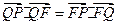 得:
得: ,
, ,
,  ,
,  .
.所以点
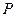 的轨迹
的轨迹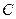 是抛物线,由题意,轨迹
是抛物线,由题意,轨迹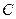 的方程为:
的方程为: .
.(Ⅱ)(1)由已知
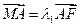 ,
,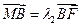 ,得
,得 .
.则
 :
: .…………①
.…………①过点
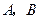 分别作准线
分别作准线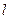 的垂线,垂足分别为
的垂线,垂足分别为 ,
, ,
,则有:
 .…………②
.…………②由①②得:
 ,即
,即 .
.(Ⅱ)(2)解:由解法一,




 .
.当且仅当
 ,即
,即 时等号成立,所以
时等号成立,所以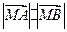 最小值为16.
最小值为16.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
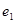 ,
,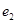 分别为具有公共焦点
分别为具有公共焦点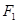 与
与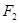 的椭圆和双曲线的离心率,
的椭圆和双曲线的离心率,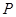 为两曲线的一个公共点,且满足
为两曲线的一个公共点,且满足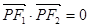 ,则
,则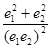 的值为
的值为 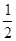
 已知点A(2,0),
已知点A(2,0),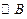
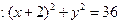 . P为
. P为 与轨迹C交于S、T两点,且
与轨迹C交于S、T两点,且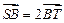 ,求直线
,求直线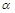 ∥
∥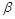 ,直线l
,直线l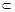
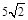 的点的轨迹是( )
的点的轨迹是( )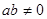 ,则方程
,则方程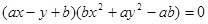 表示的曲线只可能是
表示的曲线只可能是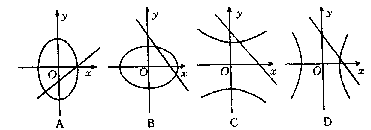
 和
和 分别表示椭轨道Ⅰ和Ⅱ的焦距,用
分别表示椭轨道Ⅰ和Ⅱ的焦距,用 和
和
 ②
② ③
③ <
< ④
④
 ,直线
,直线 :
: ,
, 为平面上的动点,过点
为平面上的动点,过点 ,且
,且 .
. 的方程;
的方程; 过定点
过定点 ,圆心
,圆心 轴交于
轴交于 、
、 两点,设
两点,设 ,
, ,求
,求 的最大值.
的最大值.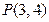 的动直线
的动直线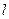 与
与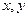 轴的交点分别为
轴的交点分别为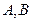 ,过
,过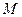 的轨迹方程为: .
的轨迹方程为: .