题目内容
已知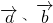 为非零向量,
为非零向量, (t∈R),若
(t∈R),若 ,当且仅当
,当且仅当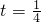 时,
时, 取得最小值,则向量
取得最小值,则向量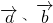 的夹角为
的夹角为
- A.

- B.

- C.

- D.

C
分析:求出向量 模的平方,通过向量的数量积得到
模的平方,通过向量的数量积得到 平方的最小值时,t的值利用
平方的最小值时,t的值利用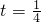 ,求出向量
,求出向量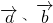 的夹角的余弦值,然后得到角的大小.
的夹角的余弦值,然后得到角的大小.
解答: 2=
2= =1+4t2+2t
=1+4t2+2t =1+4t2+4tcos
=1+4t2+4tcos ,当t=
,当t= =
= ,时取得最小值,
,时取得最小值,
所以cos =
= ,
, =
= .
.
故选C.
点评:本题是中档题,考查向量的数量积的应用,注意二次函数的最小值与三角函数值的求法,考查计算能力.
分析:求出向量
 模的平方,通过向量的数量积得到
模的平方,通过向量的数量积得到 平方的最小值时,t的值利用
平方的最小值时,t的值利用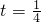 ,求出向量
,求出向量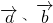 的夹角的余弦值,然后得到角的大小.
的夹角的余弦值,然后得到角的大小.解答:
 2=
2= =1+4t2+2t
=1+4t2+2t =1+4t2+4tcos
=1+4t2+4tcos ,当t=
,当t= =
= ,时取得最小值,
,时取得最小值,所以cos
 =
= ,
, =
= .
.故选C.
点评:本题是中档题,考查向量的数量积的应用,注意二次函数的最小值与三角函数值的求法,考查计算能力.

练习册系列答案
相关题目
 为非零向量,
为非零向量, (t∈R),若
(t∈R),若 ,当且仅当
,当且仅当 时,
时, 取得最小值,则向量
取得最小值,则向量 的夹角为( )
的夹角为( )



 为非零向量,
为非零向量, (t∈R),若
(t∈R),若 ,当且仅当
,当且仅当 时,
时, 取得最小值,则向量
取得最小值,则向量 的夹角为( )
的夹角为( )


