题目内容
函数y=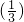
x-log2（x+2）在[-1，1]上的最大值为________．
3
分析：先判断函数的单调性，根据单调性即可求得其最大值．
解答：因为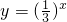
单调递减，y=log2（x+2）单调递增，
所以函数y=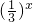
-log2（x+2）在区间[-1，1]上是单调递减函数，
所以函数的最大值是f（-1）=3．
故答案为：3．
点评：本题考查函数的单调性及其应用，考查函数在闭区间上的最值，属中档题．
分析：先判断函数的单调性，根据单调性即可求得其最大值．
解答：因为
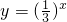单调递减，y=log2（x+2）单调递增，所以函数y=
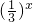-log2（x+2）在区间[-1，1]上是单调递减函数，所以函数的最大值是f（-1）=3．
故答案为：3．
点评：本题考查函数的单调性及其应用，考查函数在闭区间上的最值，属中档题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目