题目内容
已知函数f(x)=
,若y=f(x)与y=(
)x+a的图象有三个不同交点,则实数a的取值范围是( )
|
| 1 |
| 3 |
分析:作出函数的图象,由y=f(x)与y=(
)x+a的图象有三个不同交点,根据函数的图象,即可确定实数a的取值范围.
| 1 |
| 3 |
解答: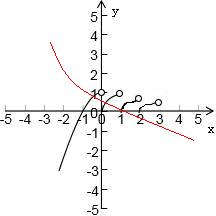 解:函数f(x)=
解:函数f(x)=
,图象如图所示,
f(x)=(
)x+a可由f(x)=(
)x变换得到,由图象可知,f(x)=(
)x+a图象经过(1,0)时,有三个交点,此时a=-
;
经过(2,0)时,有四个交点,此时a=-
,
根据图象,y=f(x)与y=(
)x+a的图象有三个不同交点时,实数a的取值范围是-
≤a<-
.
故选A.
 解:函数f(x)=
解:函数f(x)=
|
f(x)=(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
经过(2,0)时,有四个交点,此时a=-
| 1 |
| 9 |
根据图象,y=f(x)与y=(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
故选A.
点评:本题考查函数图象交点的个数问题,考查数形结合的数学思想,正确作出函数的图象是关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目