题目内容
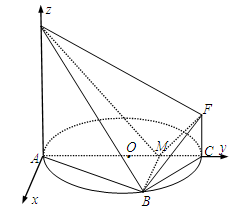
如图,AC 是圆 O 的直径,点 B 在圆 O 上,∠BAC=30°,BM⊥AC交 AC 于点 M,EA⊥平面ABC,FC//EA,AC=4,EA=3,FC=1.
(I)证明:EM⊥BF;
(II)求平面 BEF 与平面ABC 所成锐二面角的余弦值.
(Ⅰ)详见解析;(Ⅱ)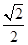 .
.
解析试题分析:(Ⅰ)先以点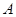 为坐标原点建立空间直角坐标系,并以此确定
为坐标原点建立空间直角坐标系,并以此确定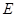 、
、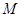 、
、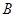 、
、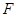 四点的坐标,通过验证
四点的坐标,通过验证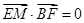 来达到证明
来达到证明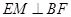 的目的;(Ⅱ)求出平面
的目的;(Ⅱ)求出平面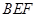 与平面
与平面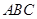 各自的法向量,利用空间向量法求出平面
各自的法向量,利用空间向量法求出平面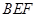 与平面
与平面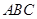 所成锐二面角的余弦值.
所成锐二面角的余弦值.
试题解析:(1)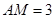 ,
,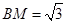 .
.
如图,以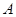 为坐标原点,垂直于
为坐标原点,垂直于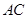 、
、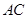 、
、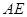 所在的直线为
所在的直线为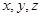 轴建立空间直角坐标系.由已知条件得
轴建立空间直角坐标系.由已知条件得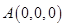 ,
, ,
,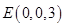 ,
,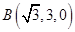 ,
,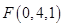 ,
,
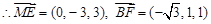 .
.
由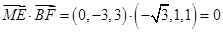 ,
,
得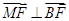 ,
, 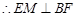 .
.
(2)由(1)知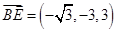 ,
,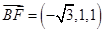 .
.
设平面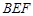 的法向量为
的法向量为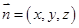 ,
,
由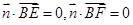 ,得
,得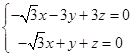 ,
,
令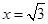 得
得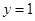 ,
,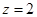 ,
,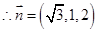 ,[来源:学+科+网]
,[来源:学+科+网]
由已知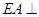 平面
平面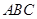 ,所以取面
,所以取面 的法向量为
的法向量为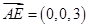 ,
,
设平面 与平面
与平面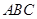 所成的锐二面角为
所成的锐二面角为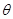 ,
,
则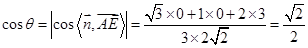 ,
,
平面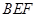 与平面
与平面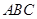 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为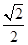 .
.
考点:直线与直线的垂直、二面角、空间向量法

练习册系列答案
相关题目
 中,四边形
中,四边形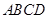 为菱形,
为菱形,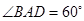 ,
,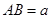 ,面
,面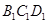 ∥面
∥面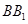 、
、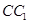 、
、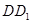 都垂直于面
都垂直于面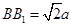 ,
,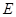 为
为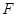 为
为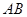 的中点.
的中点.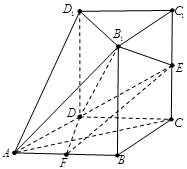
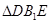 为等腰直角三角形;
为等腰直角三角形;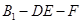 的大小.
的大小. 中,底面
中,底面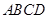 为平行四边形,侧面
为平行四边形,侧面 底面
底面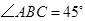 ,
,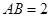 ,
,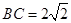 ,
,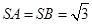 .
.
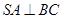 ;
;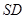 与平面
与平面 所成角的正弦值.
所成角的正弦值.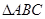 中,
中, ,
, ,
, 为
为 的中点,
的中点,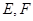 分别在线段
分别在线段 上,且
上,且
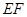 交
交 于
于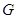 ,把
,把 沿
沿

 平面
平面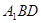 ;
; 为直二面角时,是否存在点
为直二面角时,是否存在点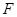 ,使得直线
,使得直线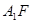 与平面
与平面 所成的角为
所成的角为 ,若存在求
,若存在求 的长,若不存在说明理由.
的长,若不存在说明理由. 的底面为平行四边形,
的底面为平行四边形,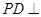 平面
平面 ,
, 为
为 中点.
中点.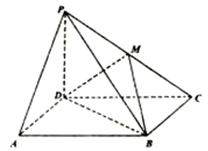
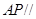 平面
平面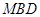 ;
;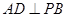 ,求证:
,求证: 平面
平面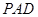 .
. 的底边
的底边 ,点
,点 在线段
在线段 上,
上, 于
于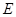 ,现将
,现将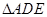 沿
沿 折起到
折起到 的位置(如图(2)).
的位置(如图(2)).
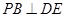 ;
; ,直线
,直线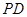 与平面
与平面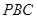 所成的角为
所成的角为 ,求
,求 长.
长.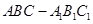 中,
中,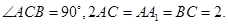

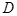 为
为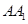 的中点,求证:平面
的中点,求证:平面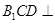 平面
平面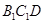 ;
;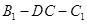 的大小为
的大小为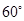 ,试确定
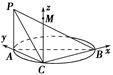
,试确定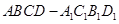 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱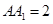 ,
,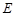 为
为 中点,
中点,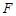 为
为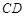 中点,
中点,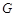 为
为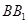 上一个动点.
上一个动点.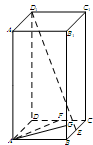
 ;
;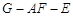 的平面角余弦值.
的平面角余弦值.