题目内容
已知函数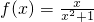
，
（1）判断f（x）的奇偶性，并证明；
（2）方程
是否有根？如果有根x0，请求出一个长度为
的区间（a，b），使x0∈（a，b），如果没有，说明为什么？（注：区间（a，b）的长度=b-a）
解：（1）函数的定义域为R．由于
，∴函数为奇函数；
（2）由题意，
，即x3+x+1=0
令g（x）=x3+x+1，则g（x）′=3x2+1≥0，即函数在R上单调增，又
，∴
分析：（1）利用f（-x）=-f（x）可判断函数为奇函数；
（2）由题意，只需判断函数的零点所在的区间长度为即可．
点评：本题考查函数的性质，考查函数零点区间的判断，属于基础题．
，∴函数为奇函数；（2）由题意，
，即x3+x+1=0令g（x）=x3+x+1，则g（x）′=3x2+1≥0，即函数在R上单调增，又
，∴分析：（1）利用f（-x）=-f（x）可判断函数为奇函数；
（2）由题意，只需判断函数的零点所在的区间长度为
即可．点评：本题考查函数的性质，考查函数零点区间的判断，属于基础题．
练习册系列答案
相关题目
，
上的单调性；
．
，求a，b的值．
．
的奇偶性；（4分）
的方程
有两解，求实数
的取值范围；（6分）
，记
，试求函数
在区间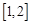
上的最大值.（10分）
．
，
的奇偶性；（2）求证：方程
至少有一根在区间