题目内容
设椭圆 ,直线
,直线 过椭圆左焦点
过椭圆左焦点 且不与
且不与 轴重合,
轴重合,  与椭圆交于
与椭圆交于 ,两点,当
,两点,当 与
与 轴垂直时,
轴垂直时, ,若点
,若点 且
且
(1)求椭圆 的方程;
的方程;
(2)直线 绕着
绕着 旋转,与圆
旋转,与圆 交于
交于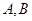 两点,若
两点,若 ,求
,求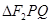 的面积
的面积 的取值范围(
的取值范围( 为椭圆的右焦点)。
为椭圆的右焦点)。
 ,直线
,直线 过椭圆左焦点
过椭圆左焦点 且不与
且不与 轴重合,
轴重合,  与椭圆交于
与椭圆交于 ,两点,当
,两点,当 与
与 轴垂直时,
轴垂直时, ,若点
,若点 且
且
(1)求椭圆
 的方程;
的方程;(2)直线
 绕着
绕着 旋转,与圆
旋转,与圆 交于
交于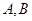 两点,若
两点,若 ,求
,求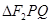 的面积
的面积 的取值范围(
的取值范围( 为椭圆的右焦点)。
为椭圆的右焦点)。(1) (2)
(2)
 (2)
(2)
直线 过椭圆左焦点
过椭圆左焦点 且不与
且不与 轴重直,当
轴重直,当 与
与 轴垂直时,
轴垂直时,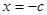 在求的纵标,想减得长度
在求的纵标,想减得长度 ;直线与圆交点弦问题:半径,弦长一半,弦心距够成用勾股定理解决,根据
;直线与圆交点弦问题:半径,弦长一半,弦心距够成用勾股定理解决,根据 ,圆心
,圆心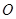 到
到 的距离
的距离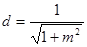 得
得 ,在表达出
,在表达出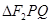 的面
的面


根据m的范围,解得 。
。
解:(1)设椭圆半焦距为 ,
, ,将
,将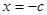 代入椭圆方程得
代入椭圆方程得 所以
所以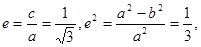
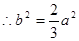
 所求椭圆方程为:
所求椭圆方程为: …………4分
…………4分
(3)设直线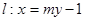 即
即 ,圆心
,圆心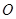 到
到 的距离
的距离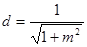
由圆性质: ,又
,又 ,得
,得 …6分
…6分
联立方程组 ,消去
,消去 得
得
设 则
则



 ,……9分
,……9分
设 ,
,
 在
在 上为增函数,
上为增函数, ,所以,
,所以,
 过椭圆左焦点
过椭圆左焦点 且不与
且不与 轴重直,当
轴重直,当 与
与 轴垂直时,
轴垂直时,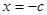 在求的纵标,想减得长度
在求的纵标,想减得长度 ;直线与圆交点弦问题:半径,弦长一半,弦心距够成用勾股定理解决,根据
;直线与圆交点弦问题:半径,弦长一半,弦心距够成用勾股定理解决,根据 ,圆心
,圆心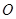 到
到 的距离
的距离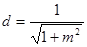 得
得 ,在表达出
,在表达出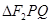 的面
的面


根据m的范围,解得
 。
。解:(1)设椭圆半焦距为
 ,
, ,将
,将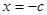 代入椭圆方程得
代入椭圆方程得 所以
所以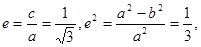
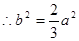
 所求椭圆方程为:
所求椭圆方程为: …………4分
…………4分(3)设直线
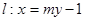 即
即 ,圆心
,圆心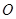 到
到 的距离
的距离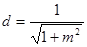
由圆性质:
 ,又
,又 ,得
,得 …6分
…6分联立方程组
 ,消去
,消去 得
得
设
 则
则



 ,……9分
,……9分设
 ,
,
 在
在 上为增函数,
上为增函数, ,所以,
,所以,

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 上一点
上一点 到右准线的距离为
到右准线的距离为 ,则该点到左焦点的距离为( )
,则该点到左焦点的距离为( ) 



 (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。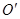 ),在斜平行光线的照射下,其阴影为一
),在斜平行光线的照射下,其阴影为一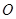 为原点,
为原点,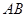 所在直线为
所在直线为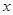 轴,设椭圆的方程为
轴,设椭圆的方程为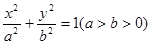 ,篮球与地面的接触点为
,篮球与地面的接触点为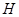 ,且
,且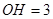 ,则椭圆的离心率为______.
,则椭圆的离心率为______.
 ,点M是线段AB上一点,且
,点M是线段AB上一点,且 点M随线段AB的滑动而运动.
点M随线段AB的滑动而运动. 的直线
的直线 交曲线E于C、D两点,交y轴于点P,若
交曲线E于C、D两点,交y轴于点P,若 的值
的值
 :
: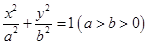 的离心率为
的离心率为 ,
,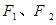 分别为椭圆
分别为椭圆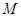 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆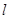 有公共点时,求△
有公共点时,求△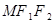 面积的最大值.
面积的最大值.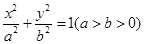 上有一点M,
上有一点M,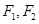 是椭圆的两个焦点,若
是椭圆的两个焦点,若 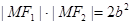 ,则椭圆离心率的范围是( )
,则椭圆离心率的范围是( )
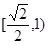

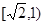
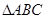 是等腰三角形,
是等腰三角形,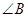 =
=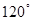 ,则以
,则以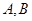 为焦点且过点
为焦点且过点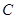 的双曲线的离心率为
的双曲线的离心率为 



 与双曲线
与双曲线 有相同的焦点, 则m的值为( )
有相同的焦点, 则m的值为( )


