题目内容
已知曲线C1:y=x2,C2:y=lnx,直线x=t与曲线C1,C2分别交于M,N两点,求|MN|最小是t的值.
∵直线x=t与曲线C1,C2分别交于M,N两点,
∴M(t,t2),N(t,lnt),
∴|MN|=|t2-ln|=t2-lntt,
令g(t)=t2-lnt(t>0),
g′(t)=2t-
=
=
,
∴g′(t)>0,t>
,
g′(t)<0,t<
,
∴当t=
时,g(t)取得极小值g(
)=
+ln2,
∵在t∈(0,+∞)时,g(t)取得唯一的极小值,故也是最小值;
∴|MN|min=g(t)min=
+ln2.
∴M(t,t2),N(t,lnt),
∴|MN|=|t2-ln|=t2-lntt,
令g(t)=t2-lnt(t>0),
g′(t)=2t-
| 1 |
| t |
| 2t2-1 |
| t |
2(t+
| ||||||||
| t |
∴g′(t)>0,t>
| ||
| 2 |
g′(t)<0,t<
| ||
| 2 |
∴当t=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∵在t∈(0,+∞)时,g(t)取得唯一的极小值,故也是最小值;
∴|MN|min=g(t)min=
| 1 |
| 2 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
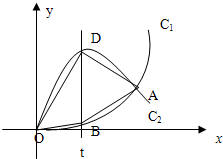 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=