题目内容
设函数 .
.
(1)若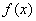 在
在 时有极值,求实数
时有极值,求实数 的值和
的值和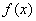 的极大值;
的极大值;
(2)若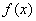 在定义域上是增函数,求实数
在定义域上是增函数,求实数 的取值范围.
的取值范围.
1)∵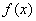 在
在 时有极值,∴有
时有极值,∴有
又 ∴
∴ , ∴
, ∴
∴有
由 得
得 ,
,
又 ∴由
∴由 得
得 或
或
由 得
得
∴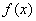 在区间
在区间 和
和 上递增,在区间
上递增,在区间 上递减
上递减
∴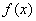 的极大值为
的极大值为
(2)若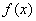 在定义域上是增函数,则
在定义域上是增函数,则 在
在 时恒成立
时恒成立

 ,
,
 需
需 时
时 恒成立,
恒成立,
化 为
为 恒成立,
恒成立,

 ,
, 
 为所求。
为所求。

练习册系列答案
相关题目
 是曲线
是曲线 的一条切线,则实数
的一条切线,则实数 __________。
__________。 恒成立,则实数
恒成立,则实数 的最小值是 ( )
的最小值是 ( ) 则
则 的大小关系为 ( )
的大小关系为 ( ) B.
B. C.
C. D.
D.
 在区间
在区间 上为减函数, 则
上为减函数, 则 的取值范围是_____,
的取值范围是_____, =(5,-3),C(-1,3),
=(5,-3),C(-1,3), =2
=2 ,若
,若 (tÎR),则
(tÎR),则 的最小值为( )
的最小值为( ) B.1 C.
B.1 C.  D.
D.
 上一点
上一点 的纵坐标为4,则点
的纵坐标为4,则点