题目内容
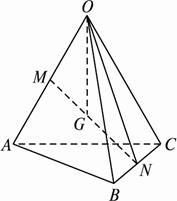
已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC.M、N分别是OA、BC的中点，G是MN的中点，求证：OG⊥BC.
证明：如图，连结ON，设∠AOB=∠BOC=∠AOC=θ，
?
又设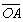
=a，
=b，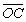
=c，则|a|=|b|=|c|，?
又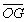
=
（
+
）=
［
+
（+
）］??
=
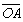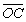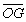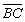（a+b+c），?
=c-b，?
∴
·
=
（a+b+c）（c-b）?
=
（a·c-a·b+b·c-b2+c2-b·c）?
=
（|a|2cosθ-|a|2cosθ-|a|2+|a|2）=0.?
∴OG⊥BC.
练习册系列答案
相关题目
，可构成空间向量的一组基底，若
，
，
，在向量已有的运算法则基础上，新定义一种运算
．显然a×b的结果仍为一向量，记作p．
平移，得到一个平行六面体
，试判断平行六面体的体积V与|(a×b)·c|的大小．
，可构成空间向量的一组基底，若
，在向量已有的运算法则基础上，新定义一种运算
．显然
的结果仍为一向量．
；
平移，得到一个平行六面体
，试判断平行六面体的体积V与
的大小关系．
