题目内容
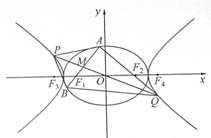
如图,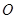 为坐标原点,椭圆
为坐标原点,椭圆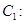
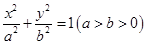 的左右焦点分别为
的左右焦点分别为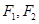 ,离心率为
,离心率为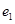 ;双曲线
;双曲线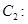
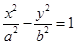 的左右焦点分别为
的左右焦点分别为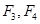 ,离心率为
,离心率为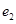 ,已知
,已知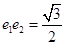 ,且
,且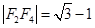 .
.
(1)求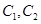 的方程;
的方程;
(2)过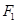 点作
点作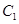 的不垂直于
的不垂直于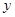 轴的弦
轴的弦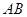 ,
,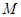 为
为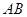 的中点,当直线
的中点,当直线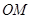 与
与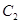 交于
交于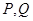 两点时,求四边形
两点时,求四边形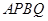 面积的最小值.
面积的最小值.
 为坐标原点,椭圆
为坐标原点,椭圆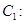
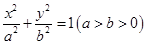 的左右焦点分别为
的左右焦点分别为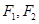 ,离心率为
,离心率为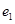 ;双曲线
;双曲线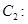
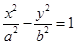 的左右焦点分别为
的左右焦点分别为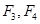 ,离心率为
,离心率为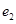 ,已知
,已知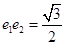 ,且
,且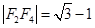 .
.(1)求
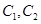 的方程;
的方程;(2)过
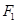 点作
点作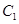 的不垂直于
的不垂直于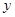 轴的弦
轴的弦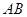 ,
,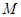 为
为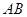 的中点,当直线
的中点,当直线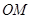 与
与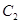 交于
交于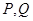 两点时,求四边形
两点时,求四边形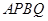 面积的最小值.
面积的最小值.
(1) 
 (2)
(2)

 (2)
(2)
试题分析:(1)利用椭圆和双曲线
 之间的关系可以用
之间的关系可以用 分别表示双曲线和椭圆的离心率和焦点,由题目
分别表示双曲线和椭圆的离心率和焦点,由题目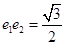 和
和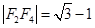 即可得到
即可得到 之间的两个方程,联立方程消元即可求出
之间的两个方程,联立方程消元即可求出 的值,得到双曲线和椭圆的标准方程.
的值,得到双曲线和椭圆的标准方程.(2)利用(1)求出焦点
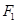 的坐标,设出弦
的坐标,设出弦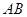 的直线的方程
的直线的方程 ,联立直线与椭圆消
,联立直线与椭圆消 得到关于
得到关于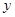 的一元二次方程,再利用根与系数的关系得到
的一元二次方程,再利用根与系数的关系得到 两点纵坐标之间的和与积,进而得到
两点纵坐标之间的和与积,进而得到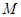 点的纵坐标带入AB直线即可得到
点的纵坐标带入AB直线即可得到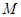 的横坐标,进而求出直线
的横坐标,进而求出直线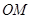 的方程,即为直线
的方程,即为直线 的方程,联立直线
的方程,联立直线 的方程
的方程 得到
得到 的取值范围和求出点
的取值范围和求出点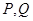 的坐标得到
的坐标得到 的长度,利用点到直线的距离得到
的长度,利用点到直线的距离得到 到直线
到直线 的距离表达式,进而用
的距离表达式,进而用 表示四边形的面积,利用不等式的性质和
表示四边形的面积,利用不等式的性质和 的取值范围即可得到面积的最小值.
的取值范围即可得到面积的最小值.(1)由题可得
 ,且
,且 ,因为
,因为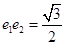 ,且
,且 ,所以
,所以 且
且
 且
且 ,所以椭圆
,所以椭圆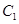 方程为
方程为 ,双曲线
,双曲线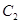 的方程为
的方程为 .
.(2)由(1)可得
 ,因为直线
,因为直线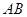 不垂直于
不垂直于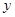 轴,所以设直线
轴,所以设直线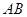 的方程为
的方程为 ,联立直线与椭圆方程可得
,联立直线与椭圆方程可得 ,则
,则 ,
, ,则
,则 ,因为
,因为 在直线
在直线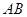 上,所以
上,所以 ,则直线
,则直线 的方程为
的方程为 ,联立直线
,联立直线 与双曲线可得
与双曲线可得
 ,
, 则
则 ,则
,则 ,设点
,设点 到直线
到直线 的距离为
的距离为 ,则
,则 到直线
到直线 的距离也为
的距离也为 ,则
,则 ,因为
,因为 在直线
在直线 的两端,所以
的两端,所以 ,
,则


 ,又因为
,又因为 在直线
在直线 上,所以
上,所以
 ,
,则四边形
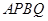 面积
面积
 ,因为
,因为 ,所以当
,所以当 时,四边形
时,四边形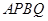 面积的最小值为
面积的最小值为 .
.
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
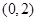 ,椭圆E:
,椭圆E: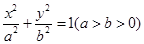 的离心率为
的离心率为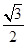 ;F是椭圆E的右焦点,直线AF的斜率为
;F是椭圆E的右焦点,直线AF的斜率为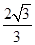 ,O为坐标原点
,O为坐标原点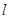 与E 相交于P,Q两点。当
与E 相交于P,Q两点。当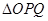 的面积最大时,求
的面积最大时,求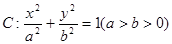 的离心率为
的离心率为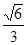 ,
,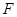 为椭圆在
为椭圆在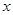 轴正半轴上的焦点,
轴正半轴上的焦点,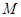 、
、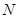 两点在椭圆
两点在椭圆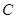 上,且
上,且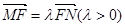 ,定点
,定点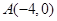 .
.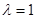 时
时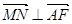 ;
;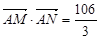 ,求椭圆
,求椭圆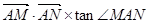 是否有最大值,若存在,求出最大值,并求出这时
是否有最大值,若存在,求出最大值,并求出这时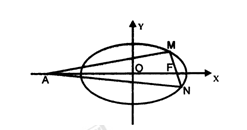
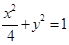 的弦
的弦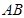 的中点为
的中点为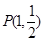 ,则弦
,则弦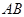 所在直线的方程是 .
所在直线的方程是 .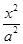 +
+ =1(a>b>0)的左顶点为A,左、右焦点分别为F1,F2,D是它短轴上的一个端点,若3
=1(a>b>0)的左顶点为A,左、右焦点分别为F1,F2,D是它短轴上的一个端点,若3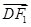 =
=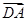 +2
+2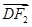 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )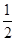

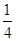
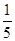
 .
. ,点B在椭圆C上,且
,点B在椭圆C上,且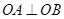 ,求线段AB长度的最小值.
,求线段AB长度的最小值. :
: ,过点
,过点
 的直线与椭圆
的直线与椭圆 、
、 两点,若点
两点,若点 的中点,则直线
的中点,则直线 的左右焦点,过F1的直线交椭圆于A、B两点,若
的左右焦点,过F1的直线交椭圆于A、B两点,若 ,则
,则 = _____________.
= _____________.