题目内容
如图,在直角坐标系中,点A(-1,0),B(1,0),P(x,y)(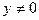 )。设
)。设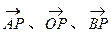 与x轴正方向的夹角分别为α、β、γ,若
与x轴正方向的夹角分别为α、β、γ,若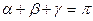 。
。
(I)求点P的轨迹G的方程;
(II)设过点C(0,-1)的直线 与轨迹G交于不同两点M、N。问在x轴上是否存在一点
与轨迹G交于不同两点M、N。问在x轴上是否存在一点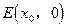 ,使△MNE为正三角形。若存在求出
,使△MNE为正三角形。若存在求出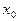 值;若不存在说明理由。
值;若不存在说明理由。
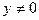 )。设
)。设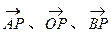 与x轴正方向的夹角分别为α、β、γ,若
与x轴正方向的夹角分别为α、β、γ,若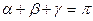 。
。(I)求点P的轨迹G的方程;
(II)设过点C(0,-1)的直线
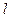 与轨迹G交于不同两点M、N。问在x轴上是否存在一点
与轨迹G交于不同两点M、N。问在x轴上是否存在一点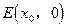 ,使△MNE为正三角形。若存在求出
,使△MNE为正三角形。若存在求出 值;若不存在说明理由。
值;若不存在说明理由。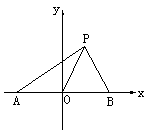
(I)轨迹G方程为
(II)不存在这样的点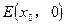 使△MNE为正△
使△MNE为正△

(II)不存在这样的点
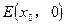 使△MNE为正△
使△MNE为正△(I)由已知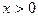 ,当
,当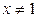 时,
时,
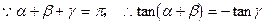
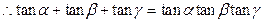
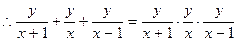
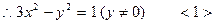
当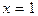 时,
时,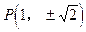 ,也满足方程<1>
,也满足方程<1>
∴所求轨迹G方程为
(II)假设存在点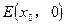 ,使
,使 为正△
为正△
设直线 方程:
方程: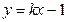 代入
代入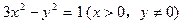
得: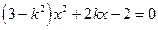
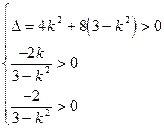
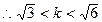
∴MN中点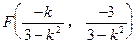
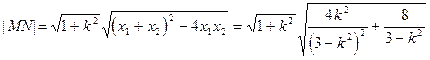
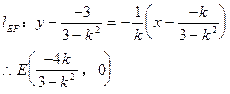
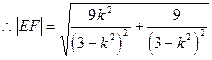
在正△EMN中,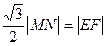
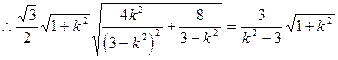
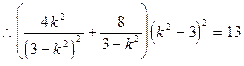
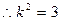 与
与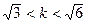 矛盾
矛盾
∴不存在这样的点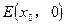 使△MNE为正△
使△MNE为正△
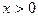 ,当
,当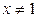 时,
时,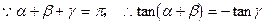
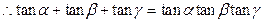
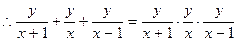
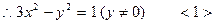
当
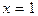 时,
时,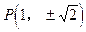 ,也满足方程<1>
,也满足方程<1>∴所求轨迹G方程为

(II)假设存在点
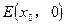 ,使
,使 为正△
为正△设直线
 方程:
方程: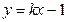 代入
代入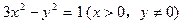
得:
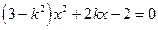
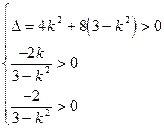
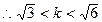
∴MN中点
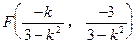
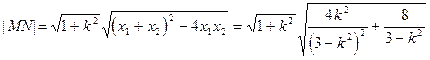
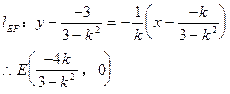
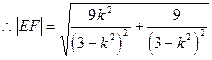
在正△EMN中,
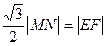
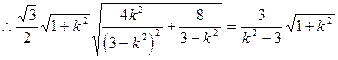
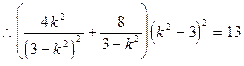
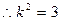 与
与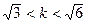 矛盾
矛盾∴不存在这样的点
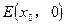 使△MNE为正△
使△MNE为正△
练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 ,是否存在斜率为k(k≠0)的直线
,是否存在斜率为k(k≠0)的直线 ,使
,使 的垂直平分线经过点M(0,-1),求斜率k的取值范围.
的垂直平分线经过点M(0,-1),求斜率k的取值范围.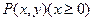 到定点
到定点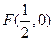 的距离比它到
的距离比它到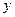 轴的距离大
轴的距离大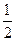 .记点
.记点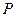 的轨迹为曲线
的轨迹为曲线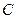
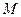 过
过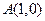 ,且圆心
,且圆心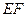 是圆
是圆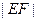 是否为定值?请说明理由.
是否为定值?请说明理由.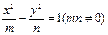 的离心率为2,有一个焦点与椭圆
的离心率为2,有一个焦点与椭圆 的焦点重合,则m的值为( )
的焦点重合,则m的值为( )



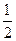 |AA1|.椭圆的一条弦AC交双曲线于E,设
|AA1|.椭圆的一条弦AC交双曲线于E,设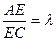 ,当
,当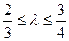 时,求双曲线的离心率e的取值范围.
时,求双曲线的离心率e的取值范围.
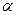 的始边为x轴的非负半轴,终边为射线l:y=
的始边为x轴的非负半轴,终边为射线l:y=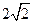 x (x≥0).
x (x≥0).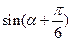 的值;
的值;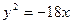 上,圆A与y轴相切,又与另一圆
上,圆A与y轴相切,又与另一圆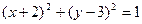 相外切,求圆A的方程.
相外切,求圆A的方程.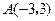 发出的光线
发出的光线 射到
射到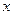 轴上,被
轴上,被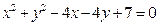 相切,求反射光线所在直线的方程.
相切,求反射光线所在直线的方程.