题目内容
(2012•泰州二模)各项均为正数的等比数列{an}满足a1a7=4,a6=8,若函数f(x)=a1x+a2x2+a3x3+…+a10x10的导数为f′(x),则f′(
)=
.
| 1 |
| 2 |
| 55 |
| 4 |
| 55 |
| 4 |
分析:利用等比数列和等差数列的通项公式、导数的运算法则即可得出.
解答:解:由各项均为正数的等比数列{an}满足a1a7=4,a6=8,设公比为q>0,于是
,解得
,
∴an=
×2n-1=2n-3.
∴f′(x)=a1+2a2x+3a3x2+…+10a10x9,
∵nan(
)n-1=n×2n-3×21-n=
,
∴f′(
)=
+
+…+
=
×
=
.
故答案为
.
|
|
∴an=
| 1 |
| 4 |
∴f′(x)=a1+2a2x+3a3x2+…+10a10x9,
∵nan(
| 1 |
| 2 |
| n |
| 4 |
∴f′(
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 4 |
| 10 |
| 4 |
| 10×11 |
| 2 |
| 1 |
| 4 |
| 55 |
| 4 |
故答案为
| 55 |
| 4 |
点评:熟练掌握等比数列和等差数列的通项公式、导数的运算法则是解题的关键.

练习册系列答案
相关题目
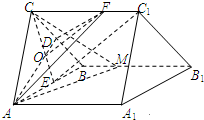 (2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
(2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.