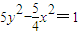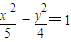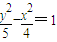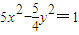题目内容
已知双曲线x2-4y2=4上一点P到双曲线的一个焦点的距离等于6,那么P点到另一焦点的距离等于 .
【答案】分析:首先将双曲线方程化成标准方程,从而得出参数a、b的值,然后根据双曲线的定义得出||PF1|-|PF2||=2a=4,根据题中的已知数据,可以求出点P到另一个焦点的距离.
解答:解:将双曲线x2-4y2=4化成标准形式: -y2=1
-y2=1
∴a2=4,b2=1
P到它的一个焦点的距离等于6,设PF1=6
∵||PF1|-|PF2||=2a=4
∴|PF2|=|PF1|±4=10或2
故答案为:10或2.
点评:本题考查了双曲线的定义与标准方程,属于基础题.利用圆锥曲线的第一定义解题,是近几年考查的常用方式,请同学们注意这个特点.
解答:解:将双曲线x2-4y2=4化成标准形式:
 -y2=1
-y2=1∴a2=4,b2=1
P到它的一个焦点的距离等于6,设PF1=6
∵||PF1|-|PF2||=2a=4
∴|PF2|=|PF1|±4=10或2
故答案为:10或2.
点评:本题考查了双曲线的定义与标准方程,属于基础题.利用圆锥曲线的第一定义解题,是近几年考查的常用方式,请同学们注意这个特点.

练习册系列答案
相关题目
已知双曲线
-
=1的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )
| y2 |
| a2 |
| x2 |
| b2 |
A、5y2-
| ||||
B、
| ||||
C、
| ||||
D、5x2-
|
已知双曲线的一个焦点与抛物线x2=20y的焦点重合,且其渐近线的方程为3x±4y=0,则该双曲线的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
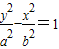 的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )
的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )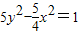
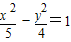
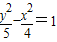
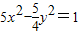
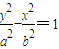 的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )
的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )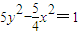
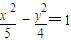
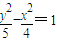
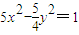
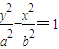 的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )
的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )