Question

    如图，已知三棱锥P—ABC中，PA⊥平面ABC，PA=3，AC=4，PB=PC=BC.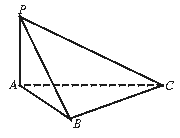

    (1)求三棱锥P—ABC的体积V；

    (2)作出点A到平面PBC的垂线段AE，并求AE的长；

    (3)求二面角A—PC—B的大小.

 

Answer 1

答案：
解析：

答案：解：(1)∵PA⊥平面ABC，PB=PC，由射影定理得，AB=AC=4.     ∵PA⊥平面ABC，∴PA⊥AC.     在Rt△PAC中，可求出PC=5，则PB=BC=5.     取BC中点D，连AD.在等腰△ABC中，求出底边上的高.     ∴.     (2)连PD，则PD⊥BC，又AD⊥BC，     ∴BC⊥平面PAD.又BC平面PBC，∴平面PAD⊥平面PBC.     作AE⊥PD于E，则AE⊥平面PBC，AE为点A到平面PBC的垂线段.     在Rt △PAD中，由PA·AD=AE·PD，即，求出.     (3)作AF⊥PC于F，连EF，由三垂线逆定理，得EF⊥PC.     ∠AFE为二面角A—PC—B的平面角.     在Rt△PAC中，由PA·AC=PC·AF，即3·4=5·AF，求出，     ∴.     即二面角A—PC—B为.