题目内容
18.O是锐角△ABC的外心,AO、BO、CO分别交对边于L、M、N,则$\frac{AO}{AL}$+$\frac{BO}{BM}$+$\frac{CO}{CN}$=2.分析 作辅助线过O作OE⊥BC交BC于E,再过A作AF⊥BC交BC于F,可得△OEL∽△AFL,得出比例式OL:AL=OE:AF,由△OBC与△ABC是同底不等高的三角形,得出AO:AL=1-S△OBC:S△ABC,同理得出BO:BM=1-S△OAC:S△BAC,CO:CN=1-S△OAB:S△CAB,三式相加即可得$\frac{AO}{AL}$+$\frac{BO}{BM}$+$\frac{CO}{CN}$的值.
解答 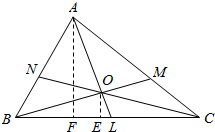 解:如图,过O作OE⊥BC交BC于E,再过A作AF⊥BC交BC于F.
解:如图,过O作OE⊥BC交BC于E,再过A作AF⊥BC交BC于F.
∵OE⊥BC,AF⊥BC,
∴OE∥AF,
∴△OEL∽△AFL,
∴OL:AL=OE:AF.
∵△OBC与△ABC是同底不等高的三角形,
∴OE:AF=S△OBC:S△ABC,
∴OL:AL=S△OBC:S△ABC,
∴1-OL:AL=1-S△OBC:S△ABC,
∴(AL-OL):AL=1-S△OBC:S△ABC,
∴AO:AL=1-S△OBC:S△ABC,…①
同理,有:BO:BM=1-S△OAC:S△BAC,…②
CO:CN=1-S△OAB:S△CAB…③
①+②+③,得:
$\frac{AO}{AL}$+$\frac{BO}{BM}$+$\frac{CO}{CN}$=3-(S△OBC+S△OAC+S△OAB):S△ABC
=3-1
=2.
故答案为:2.
点评 本题主要考查了三角形的五心中的外心,解题的关键是正确的正确的作出辅助线,利用同底不等高的三角形面积之比列出式子.

练习册系列答案
相关题目
13.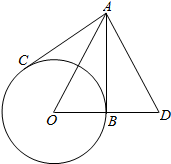 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )| A. | 70° | B. | 64° | C. | 62° | D. | 51° |
8.已知复数 $z=\frac{1-i}{i}$的共轭复数为( )
| A. | -1-i | B. | 1+i | C. | -1+i | D. | 1-i |
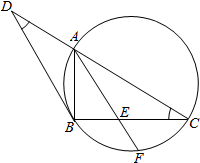 如图,BD是△ABC外接圆的切线,过A作BD的平行线交BC于E,交△ABC的外接圆于F.
如图,BD是△ABC外接圆的切线,过A作BD的平行线交BC于E,交△ABC的外接圆于F.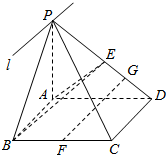 如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l.
如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l.