题目内容
已知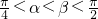 ,且
,且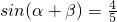 ,
, ,求sin2α,cos2β,tan2β的值.
,求sin2α,cos2β,tan2β的值.
解:∵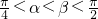 ,∴
,∴ <α+β<π,-
<α+β<π,- <α-β<0,
<α-β<0,
∴cos(α+β)=- ,sin(α-β)=-
,sin(α-β)=- ,tan(α+β)=-
,tan(α+β)=- ,tan(α-β)=-
,tan(α-β)=- ,
,
则sin2α=sin[(α+β)+(α-β)]
=sin(α+β)cos(α-β)+cos(α+β)sin(α-β)
= ×
× +(-
+(- )×(-
)×(- )
)
= ;
;
cos2β=cos[(α+β)-(α-β)]
=cos(α+β)cos(α-β)+sin(α+β)sin(α-β)
=(- )×
)× +
+ ×(-
×(- )
)
=- ;
;
tan2β=tan[(α+β)-(α-β)]
=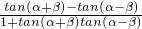
=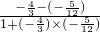
=-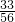 .
.
分析:根据α和β的范围,分别求出α+β和α-β的范围,利用同角三角函数间的基本关系求出cos(α+β)和sin(α-β)的值,由2α=(α+β)+(α-β),利用两角和的正弦函数公式化简sin[(α+β)+(α-β)],然后把相应的值代入可求出sin2α的值;由2β=(α+β)-(α-β),利用两角差的余弦函数公式及两角差的正切函数公式分别表示出cos[(α+β)-(α-β)]和tan[(α+β)-(α-β)],把相应的值代入即可求出cos2β与tan2β的值.
点评:此题考查了两角和与差的正弦、余弦及正切函数公式,以及同角三角函数间的基本关系,灵活变换角度,熟练掌握公式是解本题的关键.
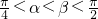 ,∴
,∴ <α+β<π,-
<α+β<π,- <α-β<0,
<α-β<0,∴cos(α+β)=-
 ,sin(α-β)=-
,sin(α-β)=- ,tan(α+β)=-
,tan(α+β)=- ,tan(α-β)=-
,tan(α-β)=- ,
,则sin2α=sin[(α+β)+(α-β)]
=sin(α+β)cos(α-β)+cos(α+β)sin(α-β)
=
 ×
× +(-
+(- )×(-
)×(- )
)=
 ;
;cos2β=cos[(α+β)-(α-β)]
=cos(α+β)cos(α-β)+sin(α+β)sin(α-β)
=(-
 )×
)× +
+ ×(-
×(- )
)=-
 ;
;tan2β=tan[(α+β)-(α-β)]
=
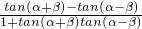
=
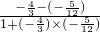
=-
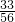 .
.分析:根据α和β的范围,分别求出α+β和α-β的范围,利用同角三角函数间的基本关系求出cos(α+β)和sin(α-β)的值,由2α=(α+β)+(α-β),利用两角和的正弦函数公式化简sin[(α+β)+(α-β)],然后把相应的值代入可求出sin2α的值;由2β=(α+β)-(α-β),利用两角差的余弦函数公式及两角差的正切函数公式分别表示出cos[(α+β)-(α-β)]和tan[(α+β)-(α-β)],把相应的值代入即可求出cos2β与tan2β的值.
点评:此题考查了两角和与差的正弦、余弦及正切函数公式,以及同角三角函数间的基本关系,灵活变换角度,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
 ,且
,且 ,
, ,求sina
.
,求sina
. ,且
,且 ,
, ,求sinβ的值.
,求sinβ的值. ,且
,且 ,
, ,求sinβ的值.
,求sinβ的值. ,且
,且 ,
, ,求sinβ的值.
,求sinβ的值.