题目内容
有4位同学参加某项选拔测试,每位同学能通过测试的概率都是 ,假设每位同学能否通过测试时相互独立的,则至少有一位同学能通过测试的概率为________.
,假设每位同学能否通过测试时相互独立的,则至少有一位同学能通过测试的概率为________.

分析:先求得其对立事件为“4为同学都不能通过测试”的概率,由对立事件的概率关系可得答案.
解答:记“至少有一位同学能通过测试”为事件A,
则其对立事件为“4为同学都不能通过测试”记为
 ,
,而每位同学不能通过测试的概率都是1-
 ,且相互独立,
,且相互独立,故P(
 )=(1-
)=(1- )4=
)4=
故P(A)=1-P(
 )=1-
)=1- =
=
故答案为:

点评:本题为独立事件的概率的求解,理清事件与事件之间的关系是解决问题的关键,属基础题.

练习册系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到了如下的2×2列联表:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
附:
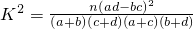
| P(K2>k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,f(1)=1,(x∈N*),猜想f(x)的表达式为
,f(1)=1,(x∈N*),猜想f(x)的表达式为


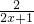
 (其中a∈R)表示的平面区域记为D,?P(x,y)∈D,z=x+y的最大值和最小值分别为M、m,已知m=-4.
(其中a∈R)表示的平面区域记为D,?P(x,y)∈D,z=x+y的最大值和最小值分别为M、m,已知m=-4. 的概率.
的概率.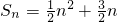 .n∈N*
.n∈N*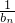 的前n项和Tn.
的前n项和Tn. 的取值范围.
的取值范围.
