题目内容
已知f(x+1)= ,f(1)=1,(x∈N*),猜想f(x)的表达式为
,f(1)=1,(x∈N*),猜想f(x)的表达式为
- A.f(x)=

- B.f(x)=

- C.f(x)=

- D.f(x)=
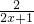
B
分析:把f(x+1)= 取倒数得
取倒数得 ,根据等差数列的定义,可知数列{
,根据等差数列的定义,可知数列{ }是以
}是以  为首项,
为首项, 为公差的等差数列,从而可求得f(x)的表达式.
为公差的等差数列,从而可求得f(x)的表达式.
解答:∵f(x+1)= ,f(1)=1,(x∈N*),
,f(1)=1,(x∈N*),
∴ .
.
∴数列{ }是以
}是以  为首项,
为首项, 为公差的等差数列.
为公差的等差数列.
∴ =
=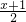 ,
,
∴f(x)= ,
,
故选B.
点评:本题主要考查抽象函数求解析式,进而转化为数列研究数列的通项,考查灵活应用知识分析解决问题的能力和运算能力,知识的迁移能力,属中档题.
分析:把f(x+1)=
 取倒数得
取倒数得 ,根据等差数列的定义,可知数列{
,根据等差数列的定义,可知数列{ }是以
}是以  为首项,
为首项, 为公差的等差数列,从而可求得f(x)的表达式.
为公差的等差数列,从而可求得f(x)的表达式.解答:∵f(x+1)=
 ,f(1)=1,(x∈N*),
,f(1)=1,(x∈N*),∴
 .
.∴数列{
 }是以
}是以  为首项,
为首项, 为公差的等差数列.
为公差的等差数列.∴
 =
=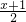 ,
,∴f(x)=
 ,
,故选B.
点评:本题主要考查抽象函数求解析式,进而转化为数列研究数列的通项,考查灵活应用知识分析解决问题的能力和运算能力,知识的迁移能力,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目