题目内容
已知:各项均为正数的数列 的前
的前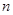 项和为
项和为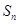 ,且对任意正整数
,且对任意正整数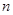 ,点
,点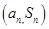 都在直线
都在直线 上.求数列
上.求数列 的通项公式;
的通项公式;
附加:若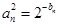 设
设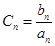 求:数列
求:数列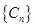 前
前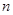 项和
项和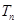 .
.
 ,
,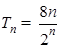 .
.
解析试题分析:由于点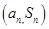 都在直线
都在直线 上,可将点代入直线方程得到
上,可将点代入直线方程得到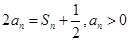 ,再根据
,再根据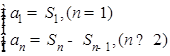 ,即可求出通项公式;
,即可求出通项公式;
附加题:根据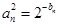 ,可得{
,可得{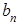 }的通项公式,进而求出{
}的通项公式,进而求出{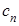 }的通项公式,再利用错位相减法求和即可求出
}的通项公式,再利用错位相减法求和即可求出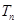 .
.
试题解析:解:由题意知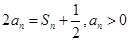 ;当
;当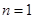 时
时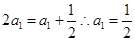
当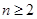 时,
时,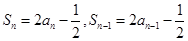 两式相减得
两式相减得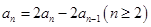
整理得: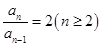
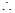 数列
数列 是
是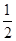 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.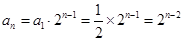 8分
8分
附加: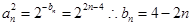
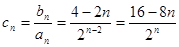 6分
6分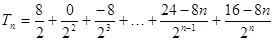 ①
①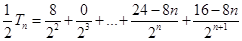 ② 7分
② 7分
① ②得
②得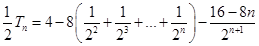
=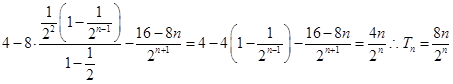 8分
8分
考点:1.数列的递推公式;2.错位相减法求和.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 中,
中,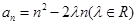 ,若
,若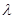 的取值范围为___________.
的取值范围为___________.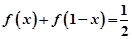 .
.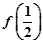 和
和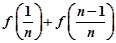 (n∈N*)的值;
(n∈N*)的值; ,求an;
,求an;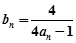 ,
,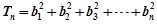 ,
,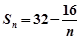 ,试比较Tn和Sn的大小。
,试比较Tn和Sn的大小。 的前
的前 项和
项和 ,且
,且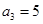 ,
,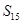 =225
=225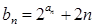 ,求数列
,求数列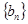 的前
的前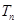 .
. 的前
的前 项和为
项和为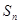 ,对一切正整数
,对一切正整数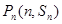 都在函数
都在函数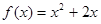 的图象上.
的图象上.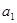 ,
,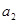 ;
;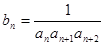 ,求证数列
,求证数列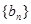 的前
的前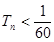 .
.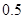 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变. ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列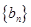 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;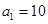
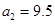
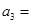
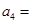
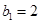

 3
3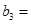
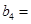
 中,
中,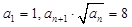 .
.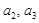 ;
;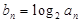 ,求证:
,求证: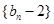 为等比数列;
为等比数列;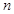 项积
项积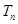 .
.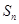 表示等差数列
表示等差数列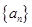 的前
的前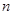 项的和,且
项的和,且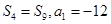
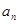 及
及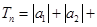 ……
……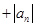
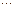 +
+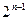 所有项的和为
所有项的和为