题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)是否存在非负整数![]() ,使得函数
,使得函数![]() 是单调函数,若存在,求出
是单调函数,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)已知![]() ,若存在
,若存在![]() ,使得当
,使得当![]() 时,
时,![]() 的最小值是
的最小值是![]() ,求实数
,求实数![]() 的取值范围.(注:自然对数的底数
的取值范围.(注:自然对数的底数![]() )
)
【答案】(1)![]() (2)存在,
(2)存在,![]() 的值是0,1,2;(3)
的值是0,1,2;(3)![]()
【解析】
(1)当![]() 时求出函数的导数,计算
时求出函数的导数,计算![]() 及
及![]() ,利用点斜式,即可求出切线方程。
,利用点斜式,即可求出切线方程。
(2)求出函数![]() 的导数,要使函数
的导数,要使函数![]() 是单调函数即是使
是单调函数即是使![]() 或
或![]() 恒成立,对
恒成立,对![]() 分类讨论,即可求出非负整数
分类讨论,即可求出非负整数![]() 的值。
的值。
(3)通过讨论![]() 的范围,根据函数的单调性求出
的范围,根据函数的单调性求出![]() 的最小值,从而确定实数
的最小值,从而确定实数![]() 的取值范围。
的取值范围。
解:(1)![]() 的定义域为
的定义域为![]() .
.
当![]() 时,
时,![]() ,
,![]() .∴
.∴![]() .
.
所以,函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
即![]()
(2)∵![]() ,∴
,∴![]() ,
,![]() .
.
当![]() 时,
时,![]() .∴
.∴![]() 是单调减函数.符合
是单调减函数.符合
当![]() 时,若
时,若![]() 是单调增函数,则
是单调增函数,则![]() ,
,
即![]() 恒成立,这不可能;
恒成立,这不可能;
若![]() 是单调减函数,则
是单调减函数,则![]() ,
,
即![]() 恒成立,令
恒成立,令![]() ,其开口方向向上,对称轴方程为
,其开口方向向上,对称轴方程为
![]() ,
,![]() ,故
,故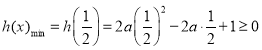 ,∴
,∴![]()
又![]() ,
,![]() .
.
综上,满足条件的非负整数![]() 的值是0,1,2
的值是0,1,2
(3)∵![]()
∴![]()
∴![]()
![]()
![]()
①当![]()
![]() 0时,
0时,![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为减函数;
上为减函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数.
上为增函数.
所以当![]()
![]() 时,
时,![]() ,不符合题意.
,不符合题意.
②当![]() 时,
时,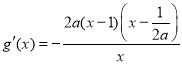 .
.
(i)当![]() ,即
,即![]() 时,当
时,当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下:
的变化情况如下:
|
|
|
| 1 |
|
| - | 0 | + | 0 | - |
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
若满足题意,只需满足![]() ,整理得
,整理得![]() .
.
令![]() ,
,
当![]() 时,
时,![]()
![]() ,
,
所以![]() 在
在![]() 上为增函数,
上为增函数,
所以,当![]() 时,
时,![]()
![]() .
.
可见,当![]() 时,
时,![]() 恒成立,故当
恒成立,故当![]() ,
,![]()
![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() .;所以
.;所以![]() 满足题意.
满足题意.
(ⅱ)当![]() ,即
,即![]() 时,
时,![]() ,,0,当且仅当
,,0,当且仅当![]() 时取等号.
时取等号.
所以![]() 在
在![]() 上为减函数.从而
上为减函数.从而![]() 在
在![]() 上为减函数.符合题意.
上为减函数.符合题意.
(ⅲ)当![]() ,即
,即![]() 时,当
时,当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
| 1 |
|
|
|
| - | 0 | + | 0 | - |
| ↘ | 极小值0 | ↗ | 极大值 | ↘ |
若满足题意,只需满足![]() ,且
,且![]() (若
(若![]() ,不符合题意),
,不符合题意),
即![]() ,且
,且![]() .
.
又![]() ,
,![]() ∴
∴![]() .
.
综上,![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了2018年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内,且月工资收入在
(百元)内,且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:
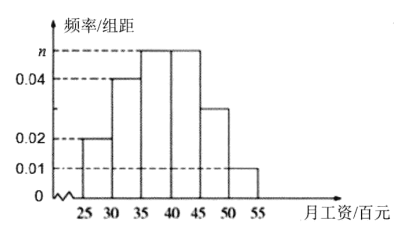
(1)求![]() 的值;
的值;
(2)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名.
名.
①完成如下所示![]() 列联表
列联表
技术工 | 非技术工 | 总计 | |
月工资不高于平均数 |
| ||
月工资高于平均数 |
| ||
总计 |
|
|
|
②则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: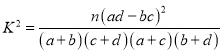 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|