题目内容
(1-x2)(x+ )6展开式中的常数项为
)6展开式中的常数项为
- A.5
- B.10
- C.15
- D.20
A
分析:将(1-x2)(x+ )6展开得到(x+
)6展开得到(x+ )6-x2(x+
)6-x2(x+ )6,将(1-x2)(x+
)6,将(1-x2)(x+ )6展开式中的常数项转化为(x+
)6展开式中的常数项转化为(x+ )6的常数项减去(x+
)6的常数项减去(x+ )6的含x-2项的系数,利用二项展开式的通项公式求出(x+
)6的含x-2项的系数,利用二项展开式的通项公式求出(x+ )6的常数项和(x+
)6的常数项和(x+ )6的含x-2项的系数,进一步求出(1-x2)(x+
)6的含x-2项的系数,进一步求出(1-x2)(x+ )6展开式中的常数项.
)6展开式中的常数项.
解答:因为(1-x2)(x+ )6
)6
=(x+ )6-x2(x+
)6-x2(x+ )6
)6
所以(1-x2)(x+ )6展开式中的常数项为
)6展开式中的常数项为
(x+ )6的常数项减去(x+
)6的常数项减去(x+ )6的含x-2项的系数,
)6的含x-2项的系数,
(x+ )6的展开式的通项为
)6的展开式的通项为
令6-2r=0得r=3,所以(x+ )6的常数项为
)6的常数项为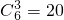 ,
,
令6-2r=-2得r=4所以(x+ )6的含x-2项的系数为
)6的含x-2项的系数为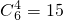 ,
,
所以(1-x2)(x+ )6展开式中的常数项为20-15=5.
)6展开式中的常数项为20-15=5.
故选A.
点评:本题考查等价转化的能力、考查利用二项展开式的通项公式解决二项展开式的特殊项问题,属于中档题.
分析:将(1-x2)(x+
 )6展开得到(x+
)6展开得到(x+ )6-x2(x+
)6-x2(x+ )6,将(1-x2)(x+
)6,将(1-x2)(x+ )6展开式中的常数项转化为(x+
)6展开式中的常数项转化为(x+ )6的常数项减去(x+
)6的常数项减去(x+ )6的含x-2项的系数,利用二项展开式的通项公式求出(x+
)6的含x-2项的系数,利用二项展开式的通项公式求出(x+ )6的常数项和(x+
)6的常数项和(x+ )6的含x-2项的系数,进一步求出(1-x2)(x+
)6的含x-2项的系数,进一步求出(1-x2)(x+ )6展开式中的常数项.
)6展开式中的常数项.解答:因为(1-x2)(x+
 )6
)6=(x+
 )6-x2(x+
)6-x2(x+ )6
)6所以(1-x2)(x+
 )6展开式中的常数项为
)6展开式中的常数项为(x+
 )6的常数项减去(x+
)6的常数项减去(x+ )6的含x-2项的系数,
)6的含x-2项的系数,(x+
 )6的展开式的通项为
)6的展开式的通项为
令6-2r=0得r=3,所以(x+
 )6的常数项为
)6的常数项为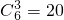 ,
,令6-2r=-2得r=4所以(x+
 )6的含x-2项的系数为
)6的含x-2项的系数为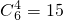 ,
,所以(1-x2)(x+
 )6展开式中的常数项为20-15=5.
)6展开式中的常数项为20-15=5.故选A.
点评:本题考查等价转化的能力、考查利用二项展开式的通项公式解决二项展开式的特殊项问题,属于中档题.

练习册系列答案
相关题目
 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足