题目内容
设A(1,0),点C是曲线y=| 1-x2 |
分析:根据∠CAO=θ条件知∠COA=180-2θ,且θ∈(
,
),写出点的坐标,点C(cos(180-2θ),sin(180-2θ)),用诱导公式整理即C(-cos2θ,sin2θ),表示出两个线段的长度之和.
| π |
| 4 |
| π |
| 2 |
解答:解:根据∠CAO=θ条件知∠COA=180-2θ,且θ∈(
,
),
则点C(cos(180-2θ),sin(180-2θ)),
即C(-cos2θ,sin2θ),
则|AC|+|CD|=(1+cos2θ)2+sin22θ-cos2θ=-2cos2θ+2cosθ+1,θ∈(
,
).
即f(θ)=-2cos2θ+2cosθ+1,θ∈(
,
)
| π |
| 4 |
| π |
| 2 |
则点C(cos(180-2θ),sin(180-2θ)),
即C(-cos2θ,sin2θ),
则|AC|+|CD|=(1+cos2θ)2+sin22θ-cos2θ=-2cos2θ+2cosθ+1,θ∈(
| π |
| 4 |
| π |
| 2 |
即f(θ)=-2cos2θ+2cosθ+1,θ∈(
| π |
| 4 |
| π |
| 2 |
点评:本题看出函数模型的选择和应用,本题解题的关键是看出所给的函数的对应的图象是半个圆,注意诱导公式的应用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 (2013•杭州模拟)如图,由半圆x2+y2=1(y≤0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,且曲线C经过点(2,3).
(2013•杭州模拟)如图,由半圆x2+y2=1(y≤0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,且曲线C经过点(2,3).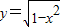 (0≤x≤1)上异于A的点,CD⊥y轴于D,,∠CAO=θ(其中O为原点),将|AC|+|CD|表示成关于θ的函数f(θ),则f(θ)= .
(0≤x≤1)上异于A的点,CD⊥y轴于D,,∠CAO=θ(其中O为原点),将|AC|+|CD|表示成关于θ的函数f(θ),则f(θ)= .