题目内容
已知点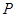 是⊙
是⊙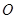 :
: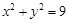 上的任意一点,过
上的任意一点,过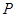 作
作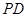 垂直
垂直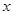 轴于
轴于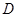 ,动点
,动点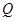 满足
满足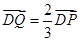 。
。
(1)求动点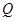 的轨迹方程;
的轨迹方程;
(2)已知点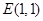 ,在动点
,在动点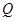 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点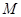 、
、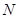 ,使
,使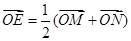 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线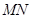 的方程,若不存在,请说明理由
的方程,若不存在,请说明理由
【答案】
(1)设 ,依题意,则点
,依题意,则点 的坐标为
的坐标为

又 
∴ 
∵  在⊙
在⊙ 上,故
上,故
∴ 
∴ 点 的轨迹方程为
的轨迹方程为
(2)假设椭圆 上存在两个不重合的两点
上存在两个不重合的两点 满足
满足
 ,则
,则 是线段MN的中点,且有
是线段MN的中点,且有
又  在椭圆
在椭圆 上
上
∴  两式相减,得
两式相减,得
 ∴
∴ 
∴ 直线MN的方程为 
∴ 椭圆上存在点 、
、 满足
满足 ,此时直线
,此时直线 的方程为
的方程为

【解析】略

练习册系列答案
相关题目
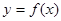 是定义在
是定义在 上的减函数,函数
上的减函数,函数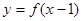 的图象关于点
的图象关于点  对称. 若对任意的
对称. 若对任意的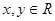 ,不等式
,不等式 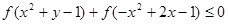 恒成立,
恒成立, 的最小值是( )
的最小值是( ) 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 是
是 轴上方椭圆
轴上方椭圆 上的一点,且
上的一点,且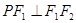 ,
,  ,
, 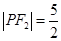 .
. 为直径的圆与以椭圆
为直径的圆与以椭圆 是椭圆
是椭圆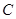 :
: 上的任意一点,
上的任意一点, 是椭圆
是椭圆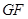 为直径的圆与以椭圆
为直径的圆与以椭圆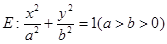 的左、右焦点分别为
的左、右焦点分别为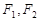 ,点
,点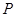 是
是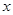 轴上方椭圆
轴上方椭圆 上的一点,且
上的一点,且 ,
, 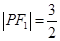 ,
, 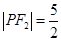 .
.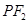 为直径的圆与以椭圆
为直径的圆与以椭圆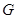 是椭圆
是椭圆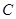 :
: 上的任意一点,
上的任意一点, 是椭圆
是椭圆 为直径的圆与以椭圆
为直径的圆与以椭圆