题目内容
三棱锥A-BCD的侧棱两两相等且相互垂直，若外接球的表面积s=8π，则侧棱的长=
．
2
| ||
| 3 |
2
| ||
| 3 |
分析：三棱锥A-BCD中，侧棱AB、AC、AD两两相等且相互垂直，补成正方体，两者的外接球是同一个，正方体的对角线就是球的直径，利用外接球的表面积s=8π，即可求出侧棱的长．
解答：解：三棱锥A-BCD中，侧棱AB、AC、AD两两相等且相互垂直，补成正方体，两者的外接球是同一个，正方体的对角线就是球的直径，设侧棱的长为a，外接球的半径为R，则
∵外接球的表面积s=8π，∴4πR2=8π
∴R=
∵正方体的对角线就是球的直径
∴
a=2
∴a=
∵外接球的表面积s=8π，∴4πR2=8π
∴R=
| 2 |
∵正方体的对角线就是球的直径
∴
| 3 |
| 2 |
∴a=
2
| ||
| 3 |
点评：本题考查球的内接几何体，考查球的表面积，解题的关键是将三棱锥转化为正方体，两者的外接球是同一个，且正方体的对角线就是球的直径．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
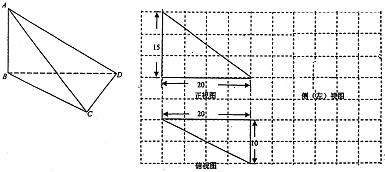如图，在三棱锥A-BCD中，AB⊥平面BCD，它的正视图和俯视图都是直角三角形，图中尺寸单位为cm．
如图，已知E、F分别是三棱锥A-BCD的侧棱AB、AD的中点，
如图空间四边形ABCD中，AC=4，BD=2，E，F分别是BC和AD的中点．
如图，将正方形ABCD沿对角线BD折成直二面角，连接A′C得到三棱锥A′-BCD，A′F 垂直BD于F，E为BC的中点．