题目内容
11.设函数f(x)=$\frac{201{5}^{x}}{201{5}^{x}+\sqrt{2015}}$.(1)求f(a)+f(1-a)的值;
(2)求f($\frac{1}{2015}$)+f($\frac{2}{2015}$)+f($\frac{3}{2015}$)+…+f($\frac{2014}{2015}$)的值.
分析 (1)由已知得f(a)+f(1-a)=$\frac{201{5}^{a}}{201{5}^{a}+\sqrt{2015}}$+$\frac{201{5}^{1-a}}{201{5}^{1-a}+\sqrt{2015}}$,由此能求出结果.
(2)由f(a)+f(1-a)=1,能求出f($\frac{1}{2015}$)+f($\frac{2}{2015}$)+f($\frac{3}{2015}$)+…+f($\frac{2014}{2015}$)的值.
解答 解:(1)∵f(x)=$\frac{201{5}^{x}}{201{5}^{x}+\sqrt{2015}}$,
∴f(a)+f(1-a)=$\frac{201{5}^{a}}{201{5}^{a}+\sqrt{2015}}$+$\frac{201{5}^{1-a}}{201{5}^{1-a}+\sqrt{2015}}$
=$\frac{201{5}^{a}}{201{5}^{a}+\sqrt{2015}}$+$\frac{2015}{2015+2015{\;}^{a+\frac{1}{2}}}$
=$\frac{201{5}^{a}}{201{5}^{a}+\sqrt{2015}}$+$\frac{\sqrt{2015}}{\sqrt{2015}+201{5}^{a}}$
=1.
(2)∵f(a)+f(1-a)=1,
∴f($\frac{1}{2015}$)+f($\frac{2}{2015}$)+f($\frac{3}{2015}$)+…+f($\frac{2014}{2015}$)
=1007×1
=1007.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,正确解题的关键是推导出f(a)+f(1-a)=1.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案| A. | 0个 | B. | 1个 | C. | 2个 | D. | 1个或2个 |
| A. | {α|90°<α<180°} | B. | {α|180°<α<270°} | ||
| C. | {α|90°+k•360°<α<180°+k•360°,k∈Z} | D. | {α|180°+k•360°<α<270°+k•360°,k∈Z} |
 (1)用弧度制表示终边在第四象限的角的集合
(1)用弧度制表示终边在第四象限的角的集合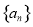 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且 是
是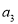 与
与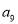 的等比中项,
的等比中项,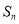 为
为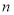 项和,则
项和,则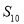 的值为( )
的值为( ) 的前
的前 项和为
项和为 ,则
,则 的最小值为( )
的最小值为( ) B.
B. C.
C. D.
D.