Question

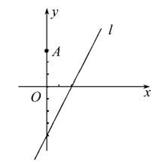
如图在平面直角坐标系xOy中，已知圆C₁：(x＋3)²＋(y－1)²＝4和圆C₂：(x－4)²＋(y－5)²＝4.

(1)若直线l过点A(4,0)，且被圆C₁截得的弦长为2，求直线l的方程；

(2)设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线l₁和l₂，它们分别与圆C₁和C₂相交，且直线l₁被圆C₁截得的弦长与直线l₂被C₂截得的弦长相等．试求所有满足条件的点P的坐标．

Answer 1

解：(1)由于直线x＝4与圆C₁不相交，所以直线l的斜率存在．设直线l的方程为y＝k(x－4)，圆C₁的圆心到直线l的距离为d，因为圆C₁被直线l截得的弦长为2，所以d＝＝1.

由点到直线的距离公式得d＝，

从而k(24k＋7)＝0，即k＝0或k＝－，

所以直线l的方程为y＝0或7x＋24y－28＝0.

(2)设点P(a，b)满足条件，不妨设直线l₁的方程为y－b＝k(x－a)，k≠0，则直线l₂的方程为y－b＝－(x－a)．因为圆C₁和C₂的半径相等，且圆C₁被直线l₁截得的弦长与圆C₂被直线l₂截得的弦长相等，所以圆C₁的圆心到直线l₁的距离和圆C₂的圆心到直线l₂的距离相等，即

＝，

整理得|1＋3k＋ak－b|＝|5k＋4－a－bk|，从而1＋3k＋ak－b＝5k＋4－a－bk或1＋3k＋ak－b＝－5k－4＋a＋bk，即(a＋b－2)k＝b－a＋3或(a－b＋8)k＝a＋b－5，因为k的取值有无穷多个，所以

或

解得或

这样点P只可能是点P₁或点P₂.

经检验点P₁和P₂满足题目条件．