题目内容
4.设集合A={x|2log${\;}_{\frac{1}{2}}$2x-21log8x+3≤0},若当x∈A时,函数f(x)=log2$\frac{x}{{2}^{a}}$•log2$\frac{x}{4}$的最大值为2,求实数a的值.分析 求解对数不等式得到log2x的范围,利用对数的运算性质化简f(x)=log2$\frac{x}{{2}^{a}}$•log2$\frac{x}{4}$,换元后分类讨论求出函数的最值,进一步求得实数a的值.
解答 解:由2log${\;}_{\frac{1}{2}}$2x-21log8x+3≤0,得$2lo{{g}_{2}}^{2}x-7lo{g}_{2}x+3≤0$,
解得:$\frac{1}{2}≤lo{g}_{2}x≤3$.
∴A={x|2log${\;}_{\frac{1}{2}}$2x-21log8x+3≤0}={x|$\frac{1}{2}≤lo{g}_{2}x≤3$},
f(x)=log2$\frac{x}{{2}^{a}}$•log2$\frac{x}{4}$=(log2x-a)(log2x-2)=$lo{{g}_{2}}^{2}x-(a+2)lo{g}_{2}x+2a$.
令t=log2x($\frac{1}{2}≤t≤3$),
则函数化为g(t)=t2-(a+2)t+2a,
其对称轴方程为t=$\frac{a+2}{2}$.
当$\frac{a+2}{2}≤\frac{7}{4}$,即$a≤\frac{3}{2}$时,g(t)max=g(3)=9-3(a+2)+2a=2,解得:a=1;
当$\frac{a+2}{2}>\frac{7}{4}$,即$a>\frac{3}{2}$时,$g(t)_{max}=g(\frac{1}{2})=\frac{1}{4}-\frac{1}{2}(a+2)+2a=2$,解得:a=$\frac{11}{6}$.
∴实数a的值为1,$\frac{11}{6}$.
点评 本题考查对数的运算性质,考查了利用换元法求函数的最值,体现了分类讨论的数学思想方法,是中档题.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案 在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).
在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).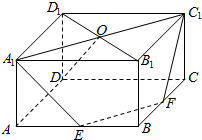 如图.在直四棱柱ABCD-A1B1C1D1中,E,F分別AB,BC的中点,A1C1与B1D1交于点O.
如图.在直四棱柱ABCD-A1B1C1D1中,E,F分別AB,BC的中点,A1C1与B1D1交于点O.