题目内容
在直三棱柱 中,
中, ,
, ,异面直线
,异面直线 与
与 所成的角等于
所成的角等于 ,设
,设 .
.

(1)求 的值;
的值;
(2)求平面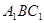 与平面
与平面 所成的锐二面角的大小.
所成的锐二面角的大小.
 中,
中, ,
, ,异面直线
,异面直线 与
与 所成的角等于
所成的角等于 ,设
,设 .
.
(1)求
 的值;
的值;(2)求平面
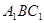 与平面
与平面 所成的锐二面角的大小.
所成的锐二面角的大小.(1)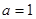 ; (2)
; (2) .
.
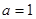 ; (2)
; (2) .
.试题分析:由于是直三棱柱,且底面是直角三角形,便于建立空间直角坐标系.
建立适当的空间直角坐标系,利用向量的夹角公式列方程,求出
 的值.
的值.在(1)的基础上,确定
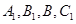 的坐标,设出平面
的坐标,设出平面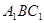 的法向量
的法向量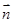 与平面
与平面 的法向量
的法向量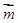 ,
,根据向量垂直的条件求出法向量,最后用向量的夹角公式求出
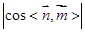 ,这就是所求锐二面角的余弦值.
,这就是所求锐二面角的余弦值.试题解析:(1)建立如图所示的空间直角坐标系,则
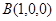 ,
,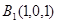 ,
,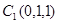 ,
,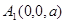 (
(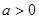 ) 1分
) 1分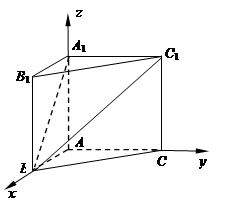
∴
 ,
,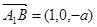 ∴
∴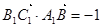 3分
3分∵异面直线
 与
与 所成的角
所成的角
∴
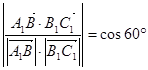 即
即 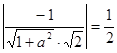 5分
5分又
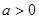 ,所以
,所以 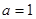 6分
6分(2)设平面
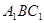 的一个法向量为
的一个法向量为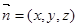 ,则
,则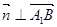 ,
,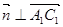 ,即
,即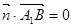 且
且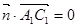
又
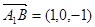 ,
,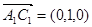
∴
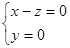 ,不妨取
,不妨取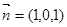 8分
8分同理得平面
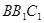 的一个法向量
的一个法向量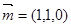 10分
10分设
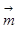 与
与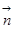 的夹角为
的夹角为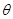 ,则
,则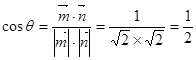 12分
12分∴
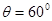 13分
13分∴平面
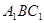 与平面
与平面 所成的锐二面角的大小为
所成的锐二面角的大小为 14分
14分
练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 中,平面
中,平面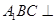 侧面
侧面 ,且
,且
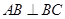 ;
; 与平面
与平面 所成的角为
所成的角为 ,求锐二面角
,求锐二面角 的大小。
的大小。

 的值.
的值. ,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
 所成角的正弦值;
所成角的正弦值; 的大小.
的大小.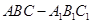 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 上的射影为
上的射影为 的中点,则异面直线
的中点,则异面直线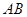 与
与 所成的角的余弦值为
所成的角的余弦值为




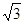 ,则异面直线AD,BC所成的角为( )
,则异面直线AD,BC所成的角为( )

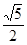
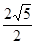


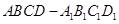 中,
中, ,则异面直线
,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )



