Question

设函数f（x）=log_ax（a＞0，a≠1），若f（x₁x₂…x₂₀₁₀）=8，则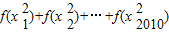的值等于    ．

Answer 1

【答案】分析：由题设条件知f（x₁²）+f（x₂²）+…+f（x₂₀₁₀²）=log_ax₁²+log_ax₂²+…+log_ax₂₀₁₀²=log_a（x₁x₂…x₂₀₁₀）²，由此能够求出f（x₁x₂…x₂₀₁₀），则可求f（x₁²）+f（x₂²）+…+f（x₂₀₁₀²）的值．
解答：解：：∵f（x）=log_ax（a＞0，a≠1），且f（x₁x₂…x₂₀₁₀）=8，
∴f（x₁²）+f（x₂²）+…+f（x₂₀₁₀²）
=log_ax₁²+log_ax₂²+…+log_ax₂₀₁₀²
=log_a（x₁x₂…x₂₀₁₀）²
=2f（x₁x₂…x₂₀₁₀）=2×8=16．
故答案为 16．
点评：本题考查对数的运算性质，解题时要注意公式的灵活运用，属于中档题．