题目内容
(本题满分14分)
设数列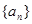 的前项
的前项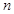 和为,已知
和为,已知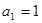 ,
,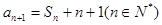 ,
,
(1)求数列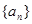 的通项公式;
的通项公式;
(2)若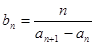 ,数列
,数列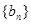 的前项和为
的前项和为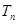 ,
,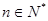 证明:
证明: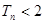 .
.
设数列
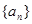 的前项
的前项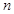 和为,已知
和为,已知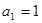 ,
,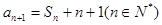 ,
,(1)求数列
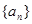 的通项公式;
的通项公式;(2)若
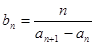 ,数列
,数列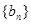 的前项和为
的前项和为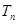 ,
,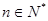 证明:
证明: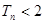 .
.(1)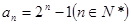 ;
;
(2)见解析
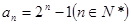 ;
;(2)见解析
(1)根据当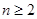 时
时
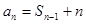 ,再与
,再与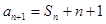 作差,可得到
作差,可得到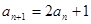 ,然后构造等比数列求通项即可.
,然后构造等比数列求通项即可.
(2)在(1)的基础上,可求出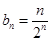 ,从而再采用错位相减的方法求和即可.
,从而再采用错位相减的方法求和即可.
解:(1)∵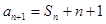 ,当
,当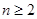 时
时
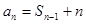 ,
,
两式相减得: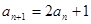 ………2分
………2分
∴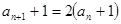 即
即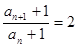 ……………4分
……………4分
又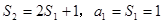 ∴
∴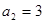 ∴
∴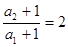 ; ………6分
; ………6分
所以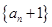 是2为首项2为公比的等比数列;
是2为首项2为公比的等比数列;
∴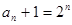 即
即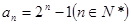 ……7分
……7分
(2)∵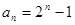 ∴
∴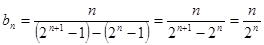 ………9分
………9分
∴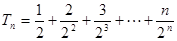
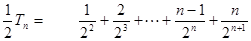 ……………10分
……………10分
∴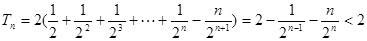 ……………14分
……………14分
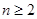 时
时
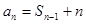 ,再与
,再与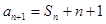 作差,可得到
作差,可得到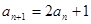 ,然后构造等比数列求通项即可.
,然后构造等比数列求通项即可.(2)在(1)的基础上,可求出
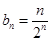 ,从而再采用错位相减的方法求和即可.
,从而再采用错位相减的方法求和即可.解:(1)∵
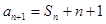 ,当
,当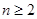 时
时
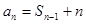 ,
,两式相减得:
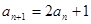 ………2分
………2分∴
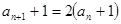 即
即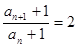 ……………4分
……………4分又
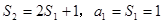 ∴
∴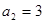 ∴
∴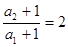 ; ………6分
; ………6分所以
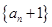 是2为首项2为公比的等比数列;
是2为首项2为公比的等比数列;∴
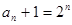 即
即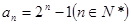 ……7分
……7分(2)∵
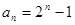 ∴
∴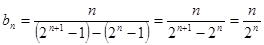 ………9分
………9分∴
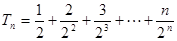
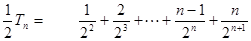 ……………10分
……………10分∴
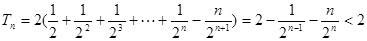 ……………14分
……………14分
练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
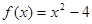 ,设曲线y=f(x)在点
,设曲线y=f(x)在点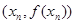 处的切线与x轴的交点为
处的切线与x轴的交点为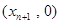 ,(
,(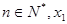 为正数)
为正数)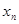 表示
表示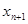
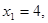 记
记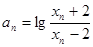 ,证明
,证明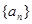 是等比数列,并求数列
是等比数列,并求数列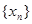 的通项公式;
的通项公式;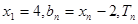 是数列
是数列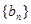 的前n项和,证明:
的前n项和,证明: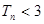
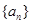 、
、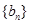 前
前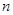 项和分别为
项和分别为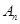 、
、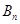 ,满足
,满足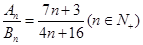 ,
,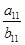 的值为( )
的值为( )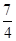
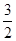
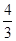
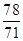
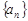 的前
的前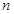 项和为
项和为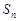 ,
,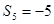 ,
,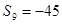 ,则
,则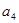 的值为( )
的值为( ) 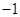
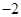
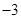
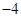
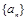 中,
中,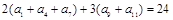 ,则此数列前13项的和
,则此数列前13项的和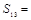 ( )
( )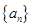 中,
中,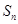 为
为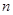 项和,
项和,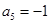 ,
,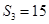 .
.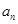 与
与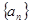 中,
中,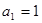 ,且
,且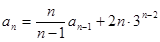 (
(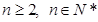 )。
)。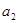 ,
,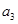 的值及数列
的值及数列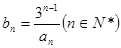 ,数列
,数列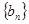 的前
的前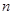 项和为
项和为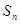 ,试比较
,试比较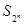 与
与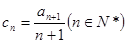 ,数列
,数列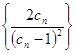 的前
的前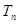 ,求证:对任意
,求证:对任意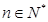 ,都有
,都有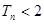 。
。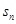 是等差数列{
是等差数列{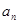 }的前n项和,已知
}的前n项和,已知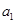 =3,
=3,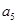 =11,则
=11,则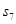 等于_________
等于_________ ,
, ,
, ,则
,则