题目内容
已知函数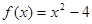 ,设曲线y=f(x)在点
,设曲线y=f(x)在点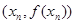 处的切线与x轴的交点为
处的切线与x轴的交点为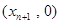 ,(
,(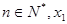 为正数)
为正数)
(1)试用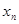 表示
表示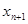
(2)若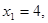 记
记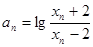 ,证明
,证明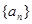 是等比数列,并求数列
是等比数列,并求数列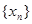 的通项公式;
的通项公式;
(3)若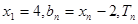 是数列
是数列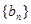 的前n项和,证明:
的前n项和,证明: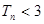
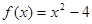 ,设曲线y=f(x)在点
,设曲线y=f(x)在点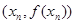 处的切线与x轴的交点为
处的切线与x轴的交点为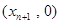 ,(
,(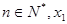 为正数)
为正数)(1)试用
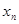 表示
表示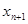
(2)若
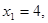 记
记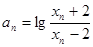 ,证明
,证明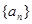 是等比数列,并求数列
是等比数列,并求数列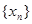 的通项公式;
的通项公式;(3)若
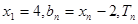 是数列
是数列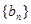 的前n项和,证明:
的前n项和,证明: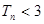
(1)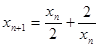 (2)
(2)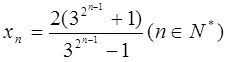 (3)见解析
(3)见解析
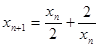 (2)
(2)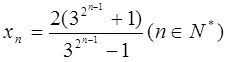 (3)见解析
(3)见解析本试题主要是考查了数列与函数,以及不等式的综合运用。
(1)因为曲线y=f(x)在点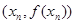 处的切线与x轴的交点为
处的切线与x轴的交点为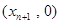 ,利用求出切点的斜率和点到坐标表示切线方程,进而得到结论。
,利用求出切点的斜率和点到坐标表示切线方程,进而得到结论。
(2)由(1)知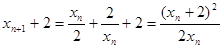 ,
,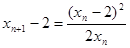
所以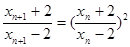 从而得到所证明数列是等比数列。
从而得到所证明数列是等比数列。
(3)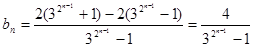 显然
显然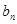 恒大于0 ------------11分
恒大于0 ------------11分
因为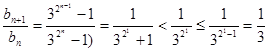
所以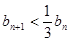
然后分类讨论求和得到证明。
解:(1)因为 所以曲线y=f(x)在点
所以曲线y=f(x)在点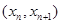 处的切线方程是
处的切线方程是 , ---------2分
, ---------2分
令y=0得
显然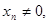 所以
所以
即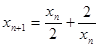 (或
(或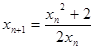 ) ----------4分
) ----------4分
(2)由(1)知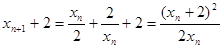 ,
,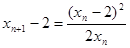
所以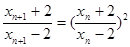 ------------6分
------------6分
从而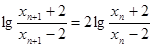 ,即
,即 其
其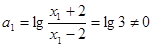
所以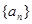 是以
是以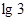 为首项,
为首项,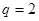 为公比的等比数列 -------8分
为公比的等比数列 -------8分
所以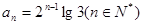 ,即
,即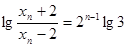
所以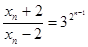 ,所以
,所以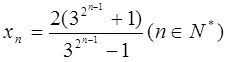 ---------10分
---------10分
(3)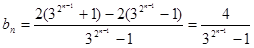 显然
显然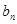 恒大于0 ------11分
恒大于0 ------11分
因为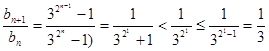
所以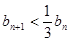 ----------12分
----------12分
当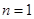 时,显然
时,显然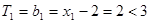
当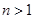 时,
时,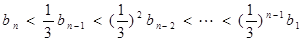
所以
即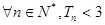 成立,证毕 ------------14分
成立,证毕 ------------14分
(1)因为曲线y=f(x)在点
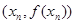 处的切线与x轴的交点为
处的切线与x轴的交点为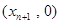 ,利用求出切点的斜率和点到坐标表示切线方程,进而得到结论。
,利用求出切点的斜率和点到坐标表示切线方程,进而得到结论。(2)由(1)知
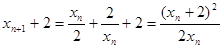 ,
,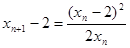
所以
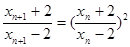 从而得到所证明数列是等比数列。
从而得到所证明数列是等比数列。(3)
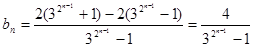 显然
显然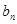 恒大于0 ------------11分
恒大于0 ------------11分因为
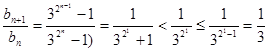
所以
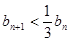
然后分类讨论求和得到证明。
解:(1)因为
 所以曲线y=f(x)在点
所以曲线y=f(x)在点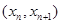 处的切线方程是
处的切线方程是 , ---------2分
, ---------2分令y=0得

显然
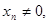 所以
所以
即
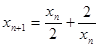 (或
(或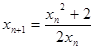 ) ----------4分
) ----------4分(2)由(1)知
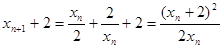 ,
,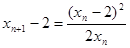
所以
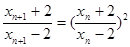 ------------6分
------------6分从而
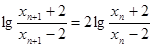 ,即
,即 其
其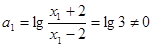
所以
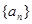 是以
是以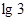 为首项,
为首项,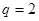 为公比的等比数列 -------8分
为公比的等比数列 -------8分所以
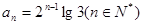 ,即
,即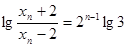
所以
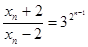 ,所以
,所以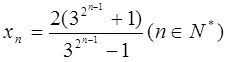 ---------10分
---------10分(3)
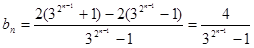 显然
显然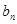 恒大于0 ------11分
恒大于0 ------11分因为
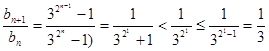
所以
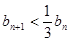 ----------12分
----------12分当
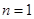 时,显然
时,显然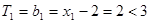
当
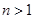 时,
时,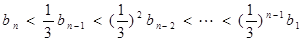
所以

即
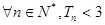 成立,证毕 ------------14分
成立,证毕 ------------14分
练习册系列答案
相关题目
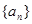 的前项
的前项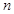 和为,已知
和为,已知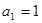 ,
,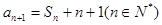 ,
,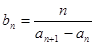 ,数列
,数列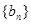 的前项和为
的前项和为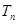 ,
,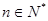 证明:
证明: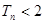 .
.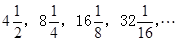 ,的前
,的前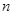 项和为( )
项和为( )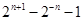
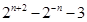

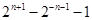
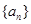 是一个等差数列,且
是一个等差数列,且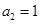 ,
,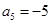 .(1)求
.(1)求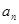 ;
;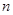 项和
项和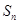 ;
;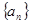 中,设
中,设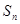 为前
为前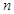 项和,且
项和,且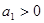 ,
,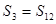 ,当
,当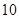

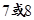

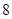
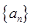 的首项为
的首项为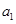 ,公差为
,公差为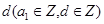 ,前
,前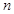 项的和为
项的和为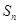 ,
,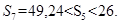
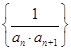 的前
的前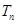 ,求
,求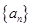 的前
的前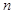 项和为
项和为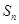 ,则下列说法错误的是 .
,则下列说法错误的是 .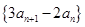 是等差数列;
是等差数列;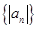 是等差数列;
是等差数列;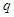 的等比数列,则
的等比数列,则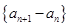 也是等比数列且公比为
也是等比数列且公比为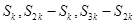
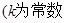
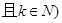 也是等比数列且公比为
也是等比数列且公比为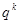 .
.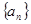 的前n项和
的前n项和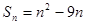 ,第k项满足
,第k项满足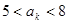 ,则k=_______
,则k=_______