题目内容
已知向量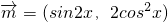 ,
,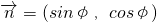 其中0<φ<π,函数
其中0<φ<π,函数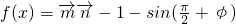 的一个零点是
的一个零点是 .
.
(1)求φ的值;
(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在
,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在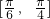 上的最大值和最小值.
上的最大值和最小值.
解:(1)∵向量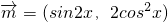 ,
,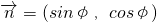
∴函数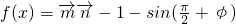 =sin2xsinφ+2cos2xcosφ-1-cosφ
=sin2xsinφ+2cos2xcosφ-1-cosφ
=sin2xsinφ+cos2xcosφ-1=sin(2x+φ)-1
∵函数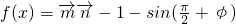 的一个零点是
的一个零点是 .
.
∴sin(2× +φ)-1=0,
+φ)-1=0,
∴φ=
(2)由上一问可以得到f(x)=sin(2x+ )-1
)-1
将函数y=f(x)的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数y=g(x)的图象
,纵坐标不变,得到函数y=g(x)的图象
∴g(x)=sin(4x+ )-1
)-1
∵ ,
,
∴4x+

∴g(x)的值域是[ ]
]
即函数的最大值是- ,最小值是-
,最小值是-
分析:(1)根据所给的向量的坐标和函数式,写出f(x)的表达式,根据函数有一个零点,把x的值代入求出φ.也得到了函数的解析式.
(2)根据上一问所得的函数解析式,写出经过平移以后的解析式,根据所给的函数的自变量的取值,做出函数的值域,写出函数的最大值和最小值.
点评:本题考查确定函数的解析式,本题解题的关键是对所给的函数式的整理,这是后面能够做对题目的关键之处,本题是一个综合题目.
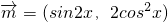 ,
,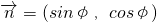
∴函数
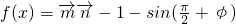 =sin2xsinφ+2cos2xcosφ-1-cosφ
=sin2xsinφ+2cos2xcosφ-1-cosφ=sin2xsinφ+cos2xcosφ-1=sin(2x+φ)-1
∵函数
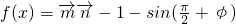 的一个零点是
的一个零点是 .
.∴sin(2×
 +φ)-1=0,
+φ)-1=0,∴φ=

(2)由上一问可以得到f(x)=sin(2x+
 )-1
)-1将函数y=f(x)的图象上各点的横坐标缩短到原来的
 ,纵坐标不变,得到函数y=g(x)的图象
,纵坐标不变,得到函数y=g(x)的图象∴g(x)=sin(4x+
 )-1
)-1∵
 ,
,∴4x+


∴g(x)的值域是[
 ]
]即函数的最大值是-
 ,最小值是-
,最小值是-
分析:(1)根据所给的向量的坐标和函数式,写出f(x)的表达式,根据函数有一个零点,把x的值代入求出φ.也得到了函数的解析式.
(2)根据上一问所得的函数解析式,写出经过平移以后的解析式,根据所给的函数的自变量的取值,做出函数的值域,写出函数的最大值和最小值.
点评:本题考查确定函数的解析式,本题解题的关键是对所给的函数式的整理,这是后面能够做对题目的关键之处,本题是一个综合题目.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 ,其中x>0.若
,其中x>0.若 ,则x的值为( )
,则x的值为( )