题目内容
已知函数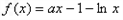
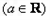 .
.
(Ⅰ)讨论函数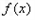 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(Ⅱ)若函数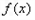 在
在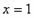 处取得极值,对
处取得极值,对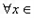
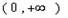 ,
,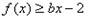 恒成立,求实数
恒成立,求实数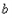 的取值范围;
的取值范围;
(Ⅲ)当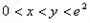 且
且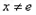 时,试比较
时,试比较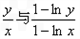 的大小.
的大小.
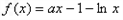
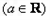 .
.(Ⅰ)讨论函数
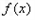 在定义域内的极值点的个数;
在定义域内的极值点的个数;(Ⅱ)若函数
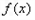 在
在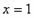 处取得极值,对
处取得极值,对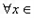
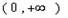 ,
,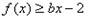 恒成立,求实数
恒成立,求实数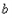 的取值范围;
的取值范围;(Ⅲ)当
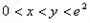 且
且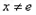 时,试比较
时,试比较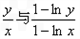 的大小.
的大小.解:(Ⅰ)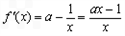 ,
,
当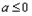 时,
时,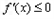 在
在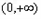 上恒成立,函数
上恒成立,函数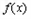 在
在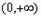 单调递减,
单调递减,
∴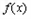 在
在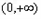 上没有极值点;
上没有极值点;
当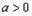 时,
时,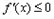 得
得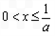 ,
,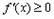 得
得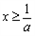 ,
,
∴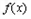 在
在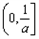 上递减,在
上递减,在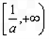 上递增,即
上递增,即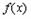 在
在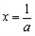 处有极小值.
处有极小值.
∴当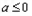 时
时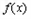 在
在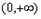 上没有极值点,
上没有极值点,
当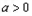 时,
时,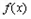 在
在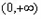 上有一个极值点.
上有一个极值点.
(Ⅱ)∵函数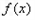 在
在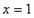 处取得极值,
处取得极值,
∴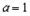 ,
,
∴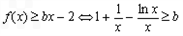 ,
,
令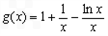 ,可得
,可得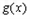 在
在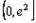 上递减,在
上递减,在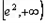 上递增,
上递增,
∴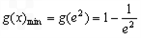 ,即
,即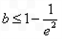 .
.
(Ⅲ)解:令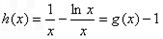 ,
,
由(Ⅱ)可知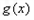 在
在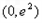 上单调递减,则
上单调递减,则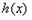 在
在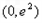 上单调递减
上单调递减
∴当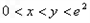 时,
时,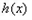 >
>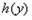 ,即
,即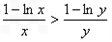 .
.
当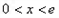 时,
时,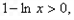
∴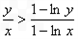 ,
,
当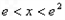 时,
时,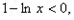
∴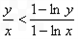

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
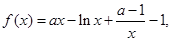 试讨论
试讨论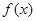 的单调性.
的单调性.
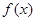 的单调区间;
的单调区间;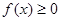 对定义域内的任意
对定义域内的任意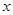 恒成立,求实数
恒成立,求实数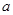 的取值范围.
的取值范围.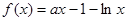 .
. 在定义域内的极值点的个数;
在定义域内的极值点的个数;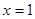 处取得极值,且对
处取得极值,且对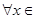
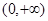 ,
,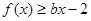 恒成立,
恒成立,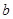 的取值范围.
的取值范围. ,讨论函数
,讨论函数 的单调区间
的单调区间