题目内容
已知函数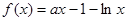 .
.
(Ⅰ)讨论函数 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(Ⅱ)已知函数 在
在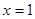 处取得极值,且对
处取得极值,且对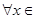
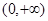 ,
,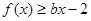 恒成立,
恒成立,
求实数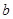 的取值范围.
的取值范围.
【答案】
(Ⅰ) 在
在 上递减,在
上递减,在 上递增,即
上递增,即 在
在 处有极小值.
处有极小值.
∴当 时
时 在
在 上没有极值点,当
上没有极值点,当 时,
时, 在
在 上有一个极值点.
上有一个极值点.
(Ⅱ) .
.
【解析】(1)求出函数的导函数,在定义域内研究其单调性就可得到极值点及其个数;(2)由函数 在
在 处取得极值,得
处取得极值,得 ,求出
,求出 .把
.把 恒成立,转化为分离参数
恒成立,转化为分离参数 求函数最值,即得
求函数最值,即得 的范围.
的范围.
(Ⅰ) ,······················································································· 1分
,······················································································· 1分
当 时,
时, 在
在 上恒成立,函数
上恒成立,函数 在
在 单调递减,
单调递减,
∴ 在
在 上没有极值点;················································································ 3分
上没有极值点;················································································ 3分
当 时,
时, 得
得 ,
, 得
得 ,
,
∴ 在
在 上递减,在
上递减,在 上递增,即
上递增,即 在
在 处有极小值.················ 5分
处有极小值.················ 5分
∴当 时
时 在
在 上没有极值点,当
上没有极值点,当 时,
时, 在
在 上有一个极值点.
上有一个极值点.
(Ⅱ)∵函数 在
在 处取得极值,∴
处取得极值,∴ ,
,
∴ ,·········································································· 8分
,·········································································· 8分
令 ,可得
,可得 在
在 上递减,在
上递减,在 上递增,··················· 10分
上递增,··················· 10分
∴ ,即
,即 . 12分
. 12分

练习册系列答案
相关题目
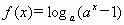 ,(
,(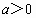 ,
,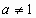 ),
),
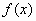 的定义域;
的定义域;
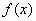 的单调性.
的单调性.