题目内容
如图,点P(0,−1)是椭圆C1:![]() (a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
(Ⅰ)求椭圆C1的方程;
(Ⅱ)求△ABD面积取最大值时直线l1的方程.

【命题意图】本题考查椭圆的几何性质,直线与圆的位置关系,直线与椭圆的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力
【答案解析】
(Ⅰ)由题意得
![]()
所以椭圆C的方程为
![]() .
.
(Ⅱ)设A(x1,y1),B(x2,y2),D(x0,y0).由题意知直线l1的斜率存在,不妨设其为k,则直线l1的方程为
y=kx−1.
又圆C2:x2+y2=4,故点O到直线l1的距离
d=![]() ,
,
所以
|AB|=2![]() =2
=2![]() .
.
又l1^l2,故直线l2的方程为
x+ky+k=0.
由

消去y,整理得
(4+k2)x2+8kx=0
故
x0=−![]() .
.
所以
|PD|=![]() .
.
设△ABD的面积为S,则
S=![]() |AB|×|PD|=
|AB|×|PD|=![]() ,
,
所以
S= £
£ =
=![]() ,
,
当且仅当k=±![]() 时取等号
时取等号
所以所求直线l1的方程为
y=±![]() x−1
x−1

练习册系列答案
相关题目
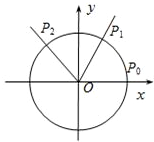 如图,点P是单位圆上的一个顶点,它从初始位置P0开始沿单位圆按逆时针方向运动角α(
如图,点P是单位圆上的一个顶点,它从初始位置P0开始沿单位圆按逆时针方向运动角α( (2013•浙江)如图,点P(0,-1)是椭圆
(2013•浙江)如图,点P(0,-1)是椭圆 如图,点P是函数y=2sin(ωx+?)(其中x∈R,
如图,点P是函数y=2sin(ωx+?)(其中x∈R,