题目内容
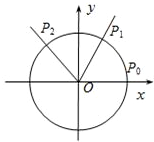如图，点P是单位圆上的一个顶点，它从初始位置P0开始沿单位圆按逆时针方向运动角α（0＜α＜| π |
| 2 |
| π |
| 3 |
| 4 |
| 5 |
分析：首先根据P2的横坐标为-
，求出cos（α+
）的值，然后根据同角三角函数的性质求出sin（α+
），最后根据cosα=cos[（α+
）-
]化简即可求出cosα．
| 4 |
| 5 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
解答：解：∵cos（α+
）=-
∴sin（α+
）=
∴cosα=cos[（α+
）-
]
=
cos(α+
) +
sin(α+
)
=
×(-
) +
×
=
；
故答案为
．
| π |
| 3 |
| 4 |
| 5 |
∴sin（α+
| π |
| 3 |
| 3 |
| 5 |
∴cosα=cos[（α+
| π |
| 3 |
| π |
| 3 |
=
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
=
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
=
3
| ||
| 10 |
故答案为
3
| ||
| 10 |
点评：本题考查单位圆与周期性，以及任意角的三角函数的定义及其应用．通过三角函数的转化来求角的余弦值．属于基础题．
练习册系列答案
相关题目
开始沿单位圆按逆时针方向运动角
（
）到达点
，然后继续沿单位圆逆时针方向运动
到达点
，若点
，则
的值等于 ▲ 
如图，点P是单位圆上的一个顶点，它从初始位置P开始沿单位圆按逆时针方向运动角α（
）到达点P1，然后继续沿单位圆逆时针方向运动
到达点P2，若点P2的横坐标为
，则cosα的值等于 ．
如图，点P是单位圆上的一个顶点，它从初始位置P开始沿单位圆按逆时针方向运动角α（
）到达点P1，然后继续沿单位圆逆时针方向运动
到达点P2，若点P2的横坐标为
，则cosα的值等于 ．
如图，点P是单位圆上的一个顶点，它从初始位置P开始沿单位圆按逆时针方向运动角α（
）到达点P1，然后继续沿单位圆逆时针方向运动
到达点P2，若点P2的横坐标为
，则cosα的值等于 ．