题目内容
(2013•东坡区一模)已知数列{an}中,a1=6,an+1=an+1,数列{bn},点(n,bn)在过点A(0,1)的直线l上,若l上有两点B、C,向量
=(1,2).
(1)求数列{an},{bn}的通项公式;
(2)设cn=2 bn,在ak与ak+1之间插入k个ck,依次构成新数列,试求该数列的前2013项之和;
(3)对任意正整数n,不等式(1+
)(1+
)•…•(1+
)-a
≥0恒成立,求正数a的范围.
| BC |
(1)求数列{an},{bn}的通项公式;
(2)设cn=2 bn,在ak与ak+1之间插入k个ck,依次构成新数列,试求该数列的前2013项之和;
(3)对任意正整数n,不等式(1+
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| n-2+an |
分析:(1)由an+1-an=1且a1=6,知an=n+5,再由已知得到
∥
,从而y=2x+1,又l过点(n,bn),推导出bn=2n+1,从而可求得.
(2)新数列:a1,c1,a2,c2,c2,a3,c3,c3,c3,a4,…,ak,ck,…,ak+1,共计有项数:k+1+
•k.经估算k=62,k+1+
•k=2016,项数接近2013,由此能求出该数列的前2013项之和.
(3)变量分离得:a≤
恒成立,由此能求出正数a的范围.
| AP |
| BC |
(2)新数列:a1,c1,a2,c2,c2,a3,c3,c3,c3,a4,…,ak,ck,…,ak+1,共计有项数:k+1+
| k+1 |
| 2 |
| k+1 |
| 2 |
(3)变量分离得:a≤
(1+
| ||||||
|
解答:解:(1)∵an+1-an=1且a1=6,∴an=n+5,…(1分)
设l上任意一点P(x,y),则
=(x,y-1),
由已知可得
∥
.
∴y=2x+1,又l过点(n,bn),
∴bn=2n+1.…(4分)
(2)新数列:a1,c1,a2,c2,c2,a3,c3,c3,c3,a4,…,ak,ck,…,ak+1,
共计项数:k+1+
•k
经估算k=62,k+1+
•k=2016,项数接近2013,…(5分)
∴S2013=(a1+a2+…+a62)+(1×c1+2×c2+…+62×c62)-2c62 …(6分)
令T=1×c1+2×c2+…+62×c62,
T=1×23+2×25+3×27+…+62×2125
4T=1×25+2×27+…+61×2125+62×2127
两式相减得:T=
…(8分)
∴S2013=
+
-2×2125=2263+
.…(9分)
(3)变量分离得:a≤
恒成立.…(10分)
令g(n)=
…(11分)
∴
=
×
=
≥1…(13分)
∵{g(n)}递增数列.
∴a∈(0,g(1))=(0,
].…(14分)
设l上任意一点P(x,y),则
| AP |
由已知可得
| AP |
| BC |
∴y=2x+1,又l过点(n,bn),
∴bn=2n+1.…(4分)
(2)新数列:a1,c1,a2,c2,c2,a3,c3,c3,c3,a4,…,ak,ck,…,ak+1,
共计项数:k+1+
| k+1 |
| 2 |
经估算k=62,k+1+
| k+1 |
| 2 |
∴S2013=(a1+a2+…+a62)+(1×c1+2×c2+…+62×c62)-2c62 …(6分)
令T=1×c1+2×c2+…+62×c62,
T=1×23+2×25+3×27+…+62×2125
4T=1×25+2×27+…+61×2125+62×2127
两式相减得:T=
| 8+185×2127 |
| 9 |
∴S2013=
| 6+67 |
| 2 |
| 8+185×2127 |
| 9 |
| 8+722×2125 |
| 9 |
(3)变量分离得:a≤
(1+
| ||||||
|
令g(n)=
(1+
| ||||||
|
∴
| g(n+1) |
| g(n) |
(1+
| ||||||||
|
| ||||||
(1+
|
=
| 2n+4 | ||||
|
∵{g(n)}递增数列.
∴a∈(0,g(1))=(0,
| 4 |
| 15 |
| 5 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,考查正数的取值范围的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
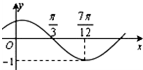 (2013•东坡区一模)函数f(x)=Asin(ωx+?)的图象如下图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象 ( )
(2013•东坡区一模)函数f(x)=Asin(ωx+?)的图象如下图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象 ( )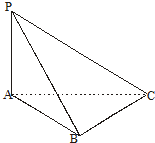 (2013•东坡区一模)三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,
(2013•东坡区一模)三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,