题目内容
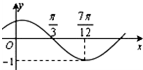（2013•东坡区一模）函数f（x）=Asin（ωx+?）的图象如下图所示，为了得到g（x）=-Acosωx的图象，可以将f（x）的图象 （ ）分析：根据函数的部分图象，看出A=1，同时得到函数四分之一周期为
，则周期T=π，求得ω=2，运用五点作图原理求得Φ，求出f（x）后，即可验证排除，也可运用诱导公式尝试．
| π |
| 4 |
解答：解：由图象看出振幅A=1，又
T=
-
=
，所以T=π，所以ω=2，再由2×
+Φ=π，得Φ=
，所以f（x）=sin（2x+
），要得到g（x）=-Acosωx=-cos2x的图象，把f（x）=sin（2x+
）中的x变为x-
，即f（x-
）=sin[2（x-
）+
]=sin（2x-
）=-cos2x．所以只要将f（x）=sin（2x+
）向右平移
个单位长度就能得到g（x）的图象．
故选B．
| 1 |
| 4 |
| 7π |
| 12 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 5π |
| 12 |
故选B．
点评：本题考查了函数f（x）=Asin（ωx+?）的图象的变换问题，解决该题的关键是先求出f（x），同时要注意图象的平移只取决于x的变化．
练习册系列答案
相关题目
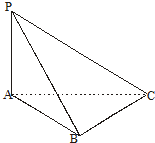（2013•东坡区一模）三棱锥P-ABC中，PA⊥平面ABC，AB⊥BC，