题目内容
(2013•东坡区一模)设x,y满足约束条件
,若目标函数z=
+
的最大值为
|
| x |
| 2 |
| y |
| 5 |
3
3
.分析:先根据约束条件画出平面区域,然后平移直线
+
=0,当过点A(4,5)时,直线在y轴上的截距最大,从而求出所求.
| x |
| 2 |
| y |
| 5 |
解答: 解:满足约束条件
解:满足约束条件
的平面区域如下图所示:
由
得A(4,5),
平移直线
+
=0,由图易得,当x=4,y=5时,
目标函数z=
+
的最大值为3.
故答案为:3.
 解:满足约束条件
解:满足约束条件
|
由
|
平移直线
| x |
| 2 |
| y |
| 5 |
目标函数z=
| x |
| 2 |
| y |
| 5 |
故答案为:3.
点评:本题考查的知识点是简单的线性规划,画出满足约束条件的可行域是关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
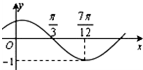 (2013•东坡区一模)函数f(x)=Asin(ωx+?)的图象如下图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象 ( )
(2013•东坡区一模)函数f(x)=Asin(ωx+?)的图象如下图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象 ( )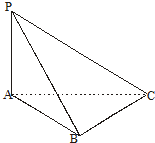 (2013•东坡区一模)三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,
(2013•东坡区一模)三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,