题目内容
16.已知t∈R,函数f(x)=$\frac{2}{x}$+tlnx.(1)当t=1时,讨论f(x)的单调性;
(2)当t>0时,若函数f(x)的最小值为g(t),求g(t)的最大值;
(3)设函数h(x)=f(x)+|(t-2)x|,x∈[1,+∞),求证:h(x)≥2.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)求出函数的导数,得到函数f(x)的最小值g(t),根据函数的单调性求出g(t)的最大值即可;
(3)求出h(x)的导数,根据函数的单调性求出h(x)的最小值即可.
解答 解:(1)t=1时,f(x)=$\frac{2}{x}$+lnx,(x>0),
f′(x)=$\frac{x-2}{{x}^{2}}$,∵x∈(0,+∞),
故f(x)在(0,2)递减,在(2,+∞)递增;
(2)当t>0时,f′(x)=$\frac{tx-2}{{x}^{2}}$=0⇒x=$\frac{2}{t}$,
x,f′(x),f(x)的变化如下:
| x | (0,$\frac{2}{t}$) | $\frac{2}{t}$ | ($\frac{2}{t}$,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
g'(t)=ln2-lnt=0⇒t=2,
t,g′(t),g(t)的变化如下:
| t | (0,2) | 2 | (2,+∞) |
| g'(t) | + | 0 | - |
| g(t) | ↗ | 极大值 | ↘ |
(3)当t≥2时,h(x)=f(x)+(t-2)x=$\frac{2}{x}$+tlnx+(t-2)x,
h′(x)=$\frac{tx-2}{{x}^{2}}$+t-2≥0,
所以h(x)在[1,+∞)上是增函数,故h(x)≥h(1)=t≥2,
当t<2时,h(x)=f(x)-(t-2)x=$\frac{2}{x}$+tlnx-(t-2)x,
h′(x)=$\frac{tx-2}{{x}^{2}}$-t+2=$\frac{[(2-t)x+2](x-1)}{{x}^{2}}$=0,
解得x=-$\frac{2}{2-t}$<0或x=1,h(x)≥h(1)=4-t>2,
综上所述:h(x)≥2.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知AD与BC是四面体ABCD中相互垂直的棱,若AD=BC=6,且∠ABD=∠ACD=60°,则四面体ABCD的体积的最大值是( )
| A. | $18\sqrt{2}$ | B. | $36\sqrt{2}$ | C. | 18 | D. | 36 |
4.已知集合A={x|(x+2)(x-3)≤0,x∈Z},B={x|(x+1)(x-1)(x-3)=0},则A∩B=( )
| A. | {-1,1} | B. | {1,3} | C. | {-1,1,3} | D. | {-3,-1,1} |
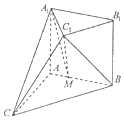 如图,在多面体ABCA1B1C1中,四边形ABB1A1是正方形,CA⊥平面ABB1A1,AC=AB=1,B1C1∥BC,BC=2B1C1.
如图,在多面体ABCA1B1C1中,四边形ABB1A1是正方形,CA⊥平面ABB1A1,AC=AB=1,B1C1∥BC,BC=2B1C1.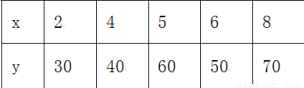
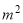 的矩形蔬菜温室.在温室内,沿左右两侧与后侧内墙各保留1
的矩形蔬菜温室.在温室内,沿左右两侧与后侧内墙各保留1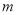 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3