题目内容
（1）已知x＞1，证明：x+
＞2；
（2）已知为a，b，c正实数，证明：a2+b2+c2≥ab+bc+ca．
| 1 | x |
（2）已知为a，b，c正实数，证明：a2+b2+c2≥ab+bc+ca．
分析：（1）利用基本不等式可以证明，注意等号不能取；
（2）利用基本不等式，在相加，即可得出结论．
（2）利用基本不等式，在相加，即可得出结论．
解答：证明：（1）∵x，
为正实数，∴x+
≥2
=2，当且仅当x=1时取等号
又∵x＞1，∴不能取等号，∴x+
＞2（6分）
（2）∵a2+b2≥2ab（当且仅当a=b时取等号），b2+c2≥2bc（当且仅当b=c时取等号），a2+c2≥2ac（当且仅当a=b时取等号），
∴2（a2+b2+c2）≥2（ab+bc+ca）（当且仅当a=b=c时取等号）
∴a2+b2+c2≥ab+bc+ca（12分）
| 1 |
| x |
| 1 |
| x |
x•
|
又∵x＞1，∴不能取等号，∴x+
| 1 |
| x |
（2）∵a2+b2≥2ab（当且仅当a=b时取等号），b2+c2≥2bc（当且仅当b=c时取等号），a2+c2≥2ac（当且仅当a=b时取等号），
∴2（a2+b2+c2）≥2（ab+bc+ca）（当且仅当a=b=c时取等号）
∴a2+b2+c2≥ab+bc+ca（12分）
点评：本题考查不等式的证明，考查基本不等式的运用，注意定理的使用条件．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
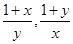中至少有一个小于2。
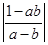>1
x∈A，试判断g（x）的单调性；（不证）