题目内容
【题目】已知函数![]()
(1)若![]() ,函数
,函数![]() 的极大值为
的极大值为![]() ,求实数
,求实数![]() 的值;
的值;
(2)若对任意的![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)第(1)问,先求导,对a分类讨论,求出每一种情况下的极大值,得到a的方程,即可求出实数a的值. (2)第(2)问,令![]() ,转化成证明g(a)的最大值小于等于
,转化成证明g(a)的最大值小于等于![]() 在
在![]() 上恒成立,再分离参数
上恒成立,再分离参数![]() 对
对![]() 恒成立
恒成立![]() ,再利用导数求右边函数的最大值得解.
,再利用导数求右边函数的最大值得解.
试题解析:
(1)∵![]() ,
,
∴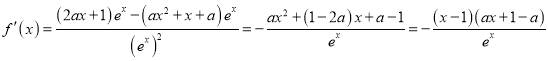
①当![]() 时,
时, ![]() ,
,
令![]() ,得
,得![]() ;
; ![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增, ![]() 上单调递减.
上单调递减.
所以![]() 的极大值为
的极大值为![]() ,不合题意.
,不合题意.
②当![]() 时,
时, ![]() ,
,
令![]() ,得
,得![]() ;
; ![]() ,得
,得![]() 或
或![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增, ![]() 和
和![]() 上单调递减.
上单调递减.
所以![]() 的极大值为
的极大值为![]() ,解得
,解得![]() .符合题意.
.符合题意.
综上可得![]() .
.
(2)令![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是增函数
上是增函数
则![]() 对
对![]() 恒成立等价于
恒成立等价于![]() ,
,
即![]() 对
对![]() 恒成立.
恒成立.
即![]() 对
对![]() 恒成立
恒成立![]()
令![]()
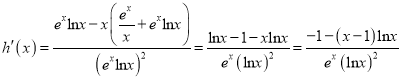
![]()
![]()
![]()
![]() 在
在![]() 上单调递减。
上单调递减。![]()
![]()
所以实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目