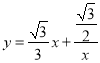题目内容
【题目】对于无穷数列![]() ,若对任意
,若对任意![]() ,满足
,满足![]() 且
且![]() (
(![]() 是与
是与![]() 无关的常数),则称数列
无关的常数),则称数列![]() 为
为![]() 数列.
数列.
(1)若![]() (
(![]() ),判断数列
),判断数列![]() 是否为
是否为![]() 数列,说明理由;
数列,说明理由;
(2)设![]() ,求证:数列
,求证:数列![]() 是
是![]() 数列,并求常数
数列,并求常数![]() 的取值范围;
的取值范围;
(3)设数列![]() (
(![]() ,
,![]() ),问数列
),问数列![]() 是否为
是否为![]() 数列?说明理由.
数列?说明理由.
【答案】(1)![]() 是
是![]() 数列,见解析;(2)
数列,见解析;(2)![]() ;证明见解析;(3)见解析.
;证明见解析;(3)见解析.
【解析】
(1)由![]() ,得到
,得到![]() ,整理后可得当
,整理后可得当![]() 为偶数时
为偶数时![]() ,进而可得得到数列
,进而可得得到数列![]() 不是
不是![]() 数列;
数列;
(2)由![]() ,得到
,得到![]() 时,
时,![]() ,此时数列
,此时数列![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,此时数列
,此时数列![]() 单调递减,得到数列
单调递减,得到数列![]() 的最大项,由此求得常数
的最大项,由此求得常数![]() 的取值范围;
的取值范围;
(3)当![]() 时,对于
时,对于![]() 有
有![]() ,可得当
,可得当![]() 时数列
时数列![]() 是
是![]() 数列,当
数列,当![]() 时,数列
时,数列![]() 不是
不是![]() 数列,当
数列,当![]() 时,数列
时,数列![]() 不是
不是![]() 数列.
数列.
(1)由![]() ,
,
可得![]() ,
,
当![]() 为偶数时,
为偶数时,![]() ,所以数列
,所以数列![]() 不是
不是![]() 数列.
数列.
(2)证明:因为![]() ,
,
所以当![]() 时,即
时,即![]() 时,
时,![]() ,此时数列
,此时数列![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,此时数列
,此时数列![]() 单调递减,
单调递减,
则数列![]() 的最大项为
的最大项为![]() ,所以
,所以![]() 的取值范围内是
的取值范围内是![]() .
.
(3)①当![]() 时,当
时,当![]() 时,
时,![]() ,
,
由![]() ,解得
,解得![]() ,
,
即当![]() 时,符合
时,符合![]() ,
,
若![]() ,则
,则![]() ,此时
,此时![]() ,
,
于是![]() ,
,
由对于![]() ,有
,有![]() ,所以当
,所以当![]() 时,数列
时,数列![]() 是
是![]() 数列;
数列;
②当![]() 时,取
时,取![]() ,则
,则![]() ,
,
由![]() ,所以当
,所以当![]() 时,数列
时,数列![]() 不是
不是![]() 数列;
数列;
③当![]() 时,取
时,取![]() ,则
,则![]() ,
,
由![]() ,所以当
,所以当![]() 时,数列
时,数列![]() 不是
不是![]() 数列.
数列.
综上可得:当![]() 时,数列
时,数列![]() 是
是![]() 数列;当
数列;当![]() 时,数列
时,数列![]() 不是
不是![]() 数列.
数列.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目