题目内容
试证明G为△ABC重心的充要条件是
证明:充分性(由![]() +
+![]() +
+![]() =0,推证G为△ABC的重心).
=0,推证G为△ABC的重心).
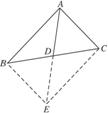
如右图,延长![]() 到D,使
到D,使![]() =
=![]() 且
且![]() 与
与![]() 交于点M,连结
交于点M,连结![]() 、
、![]() .
.
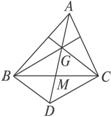
∵![]() +
+![]() +
+![]() =0,
=0,
∴![]() =-(
=-(![]() +
+![]() ),即
),即![]() =
=![]() +
+![]() .
.
又∵![]() =
=![]() ,∴
,∴![]() =
=![]() +
+![]() .
.
由向量加法的平行四边形法则知四边形GBDC为平行四边形,由于平行四边形的对角线互相平分,可知M为BC的中点,M也为GD中点,∴AM是中线且G在AM上.
又![]() =
=![]() ,
,![]() =2
=2![]() ,∴
,∴![]() =2
=2![]() .
.
∴![]() =
=![]()
![]() .∴G为△ABC的重心.
.∴G为△ABC的重心.
下面证明必要性(由G为△ABC的重心推证![]() +
+![]() +
+![]() =0).
=0).
如图,延长![]() 与
与![]() 交于D点,∴
交于D点,∴![]() 为
为![]() 边上的中线,D为
边上的中线,D为![]() 的中点.
的中点.
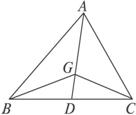
∵G是△ABC的重心,由向量加法的平行四边形法则,可知![]() +
+![]() =2
=2![]() .又由于G为△ABC的重心,
.又由于G为△ABC的重心,
∴![]() =2
=2![]() .
.
∴![]() =
=![]() +
+![]() .
.
∴-![]() +
+![]() +
+![]() =0,
=0,
即![]() +
+![]() +
+![]() =0.
=0.

练习册系列答案
相关题目

 .
. .
.