题目内容
求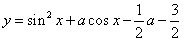 的最大值为1时a的值。
的最大值为1时a的值。
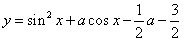 的最大值为1时a的值。
的最大值为1时a的值。解: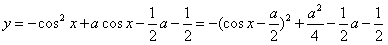 ,
,
设cosx=t,
∵-1≤cosx≤1,∴-1≤t≤1,
∴求函数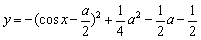 的最大值为1时a的值等价于
的最大值为1时a的值等价于
求闭区间上的二次函数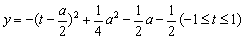 的最大值为1时a的值。
的最大值为1时a的值。
(1)当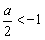 ,即a<-2时,t=-1,y有最大值为
,即a<-2时,t=-1,y有最大值为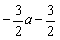 ,
,
∴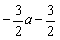 =1,∴
=1,∴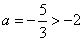 (舍去);
(舍去);
(2)当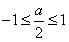 ,即-2≤a≤2时,t=
,即-2≤a≤2时,t=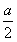 ,y有最大值为
,y有最大值为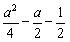 ,
,
由题设可知: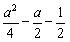 =1,解得:a=1±
=1,解得:a=1±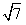 (正号舍);
(正号舍);
(3)当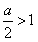 ,即a>2时,t=1,y有最大值为
,即a>2时,t=1,y有最大值为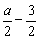 ,
,
由题设,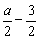 =1,∴a=5;
=1,∴a=5;
综上,a=1-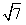 或a=5。
或a=5。
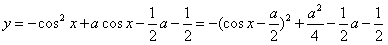 ,
,设cosx=t,
∵-1≤cosx≤1,∴-1≤t≤1,
∴求函数
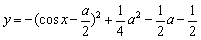 的最大值为1时a的值等价于
的最大值为1时a的值等价于求闭区间上的二次函数
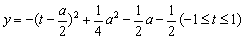 的最大值为1时a的值。
的最大值为1时a的值。(1)当
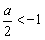 ,即a<-2时,t=-1,y有最大值为
,即a<-2时,t=-1,y有最大值为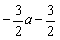 ,
,∴
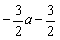 =1,∴
=1,∴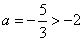 (舍去);
(舍去);(2)当
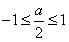 ,即-2≤a≤2时,t=
,即-2≤a≤2时,t=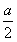 ,y有最大值为
,y有最大值为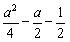 ,
,由题设可知:
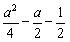 =1,解得:a=1±
=1,解得:a=1±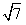 (正号舍);
(正号舍);(3)当
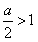 ,即a>2时,t=1,y有最大值为
,即a>2时,t=1,y有最大值为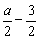 ,
,由题设,
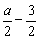 =1,∴a=5;
=1,∴a=5;综上,a=1-
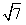 或a=5。
或a=5。 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
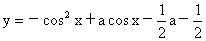 的最大值为1时a的值.
的最大值为1时a的值.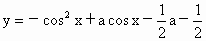 的最大值为1时a的值.
的最大值为1时a的值. a-
a-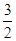 的最大值为1时a的值.
的最大值为1时a的值.