题目内容
4.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x-2y+3≥0}\\{x-3y+3≤0}\\{y-1≤0}\end{array}\right.$,若目标函数z=y-ax仅在点(-3,0)处取到最大值,则实数a的取值范围为( )| A. | (3,5) | B. | ($\frac{1}{2}$,+∞) | C. | (-1,2) | D. | ($\frac{1}{3}$,1) |
分析 根据已知的约束条件 画出满足约束条件的可行域,再用图象判断,求出目标函数的最大值
解答 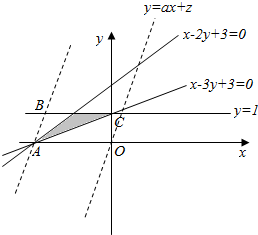 解:画出可行域如图所示,
解:画出可行域如图所示,
其中A(-3,0),C(0,1)
若目标函数z=y-ax仅在点(-3,0)取得最大值,
由图知,直线z=-ax+y的斜率大于直线x-2y+3=0的斜率,
即a>$\frac{1}{2}$
故选B.
点评 本题考查的知识点是线性规划,处理的思路为:借助于平面区域特性,用几何方法处理代数问题,体现了数形结合思想、化归思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
12.甲:“存在x∈R,使得ax2+2ax+1≤0”的否定为真.乙:0<a<1.甲是乙成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.己知集合M={x|x>1},集合N={x|x2-2x<0},则M∩N等于( )
| A. | {x|1<x<2} | B. | {x|0<x<l} | C. | {x|0<x<2} | D. | {x|x>2} |
9.若不等式组$\left\{\begin{array}{l}x≥0\\ x+3y≥4\\ 3x+y≤4\end{array}$所表示的平面区域被直线y=kx+$\frac{4}{3}$分为面积比为1:2的两部分,则k的一个值为( )
| A. | $\frac{7}{3}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | $\frac{3}{7}$ |