题目内容
已知x+x-1=3,求下列各式的值:
(1)x2+x-2
(2) .
.
解:(1)∵x+x-1=3
∴(x+x-1)2=x2+x-2+2=9
∴x2+x-2=7
(2)∵
∴ =
=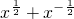
又
∴
∴
分析:(1)把已知条件平方再化简即可得解
(2)把分子看成平方差公式展开,与分母约分,再根据已知条件求解即可
点评:本题考查有利指数幂的化简,注意完全平方和公式和平方差公式的灵活应用.属简单题
∴(x+x-1)2=x2+x-2+2=9
∴x2+x-2=7
(2)∵

∴
 =
=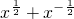
又

∴

∴

分析:(1)把已知条件平方再化简即可得解
(2)把分子看成平方差公式展开,与分母约分,再根据已知条件求解即可
点评:本题考查有利指数幂的化简,注意完全平方和公式和平方差公式的灵活应用.属简单题

练习册系列答案
相关题目
已知x+x-1=3,则x
+x-
值为( )
| 1 |
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、±
| ||
D、-
|
已知x+x-1=3,则x2+x-2值为( )
| A、11 | B、9 | C、8 | D、7 |